MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Related questions
Question
Need help with d and e
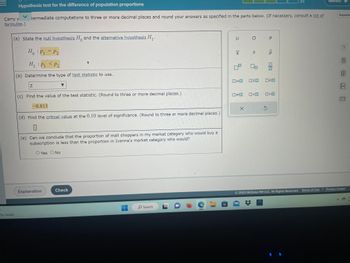
Transcribed Image Text:**Hypothesis Test for the Difference of Population Proportions**
In this educational section, we will discuss the steps involved in conducting a hypothesis test for the difference of population proportions. Follow the steps outlined below:
(a) **State the Hypotheses:**
- **Null Hypothesis (\(H_0\))**: \(p_1 = p_2\)
- **Alternative Hypothesis (\(H_1\))**: \(p_1 < p_2\)
(b) **Determine the Type of Test Statistic to Use:**
- The test statistic used in this scenario is the Z-test.
(c) **Find the Value of the Test Statistic:**
- The calculated test statistic is \(-0.813\). This value is rounded to three or more decimal places.
(d) **Find the Critical Value at the 0.10 Level of Significance:**
- The blank space indicates the need to calculate and input the critical value specific to the 0.10 significance level.
(e) **Conclusion:**
- Based on the questions posed: "Can we conclude that the proportion of mall shoppers in my market category who would buy a subscription is less than the proportion in Ivanna's market category who would?"
- Choices are provided: Yes or No.
This exercise emphasizes the importance of hypothesis testing in determining statistical differences between population proportions. Understanding the process of formulating hypotheses, selecting the right test statistic, and making conclusions based on critical values is crucial in statistical analyses.
---
**Note:** Ensure you understand how to calculate and interpret Z-scores and critical values to make informed conclusions from hypothesis tests.
![**Hypothesis Test for the Difference of Population Proportions**
Several months ago while shopping, I was interviewed to see whether or not I’d be interested in signing up for a subscription to a yoga app. I fall into the category of people who have a membership at a local gym, and guessed that, like me, many people in that category would not be interested in the app. My friend Ivanna falls in the category of people who do not have a membership at a local gym, and I was thinking that she might like a subscription to the app. After being interviewed, I looked at the interviewer’s results. Of the 98 people in my market category who had been interviewed, 17 said they would buy a subscription, and of the 120 people in Ivanna’s market category, 26 said they would buy a subscription.
Assuming that these data came from independent, random samples, can we conclude, at the 0.10 **level of significance**, that the proportion \( p_1 \) of all mall shoppers in my market category who would buy a subscription is less than the proportion \( p_2 \) of all mall shoppers in Ivanna’s market category who would buy a subscription?
Perform a **one-tailed test**. Then complete the parts below.
Carry your intermediate computations to three or more decimal places and round your answers as specified in the parts below. (If necessary, consult a list of **formulas**.)
(a) State the **null hypothesis** \( H_0 \) and the **alternative hypothesis** \( H_1 \).
\[
H_0: p_1 = p_2 \\
H_1: p_1 < p_2
\]
(b) Determine the type of **test statistic** to use.
- **Z**
(c) Find the value of the test statistic. (Round to three or more decimal places.)
- **0.813**
**Explanation**
This demonstrates a hypothesis test where the goal is to determine if there is enough statistical evidence to support the claim that one proportion is less than the other. It's an example of conducting a hypothesis test for the difference between two population proportions.
**Note: There are no graphs or diagrams associated with this text.**](https://content.bartleby.com/qna-images/question/ab310076-c445-4f02-aa72-05faca788dac/10f0cc43-49f3-4d46-bd0d-083ae2b7c01c/9gs3wy_processed.jpeg)
Transcribed Image Text:**Hypothesis Test for the Difference of Population Proportions**
Several months ago while shopping, I was interviewed to see whether or not I’d be interested in signing up for a subscription to a yoga app. I fall into the category of people who have a membership at a local gym, and guessed that, like me, many people in that category would not be interested in the app. My friend Ivanna falls in the category of people who do not have a membership at a local gym, and I was thinking that she might like a subscription to the app. After being interviewed, I looked at the interviewer’s results. Of the 98 people in my market category who had been interviewed, 17 said they would buy a subscription, and of the 120 people in Ivanna’s market category, 26 said they would buy a subscription.
Assuming that these data came from independent, random samples, can we conclude, at the 0.10 **level of significance**, that the proportion \( p_1 \) of all mall shoppers in my market category who would buy a subscription is less than the proportion \( p_2 \) of all mall shoppers in Ivanna’s market category who would buy a subscription?
Perform a **one-tailed test**. Then complete the parts below.
Carry your intermediate computations to three or more decimal places and round your answers as specified in the parts below. (If necessary, consult a list of **formulas**.)
(a) State the **null hypothesis** \( H_0 \) and the **alternative hypothesis** \( H_1 \).
\[
H_0: p_1 = p_2 \\
H_1: p_1 < p_2
\]
(b) Determine the type of **test statistic** to use.
- **Z**
(c) Find the value of the test statistic. (Round to three or more decimal places.)
- **0.813**
**Explanation**
This demonstrates a hypothesis test where the goal is to determine if there is enough statistical evidence to support the claim that one proportion is less than the other. It's an example of conducting a hypothesis test for the difference between two population proportions.
**Note: There are no graphs or diagrams associated with this text.**
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps
Knowledge Booster
Similar questions
- How many miles is the diagonal path from Jim’s house to the mall? Show your work and explain how you got your answer. (Picture below)arrow_forwardThe table shows the number of hours 9 students spent studying for a test and their scores on that test. What would be the predictable score when a student studied for 4.5 hours? Hours spent studying, x 0 2 4 5 5 5 6 7 8 Test scores, y 40 51 64 69 73 75 93 90 95 A. 67 B. 68 C. 69 D. 71arrow_forwardQ.14 1 I 1 1 7818 a b C d TRY a² b² c² d² a3 b³ c³ d³ Darrow_forward
- The data represent the heights in feet and the number of stories of the tallest buildings in a city. Height, x 793 388 825 404 439 550 931 669 532 Stories, y 57 26 58 31 33 36 60 49 34 Scatter Plot for the Heights (in Feet) and Number of Stories of the Buildings. 90- 50- 40- 30- 20- 10- 100 1200 400 300 700 Part: 0 /3 Part 1 of 3 Find the value for r. Round your answer to at least three decimal places.arrow_forward10 10 T. U V -10arrow_forwardX Frequency 12 a. Construct a histogram for the data with 7 bars 2 1 3 3 4 14 5 15 b. Describe the shape of your histogram c. What does the histogram show us? 7 10 8 5arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning 
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman