Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: 9) Find 5-2x - dx
A: Given: Find d2dx25-2x for finding second derivative, we find first derivative then find derivative…
Q: 2 So Adx 4-x
A: We can find the answer as below.
Q: S X-X dx
A:
Q: Find n when a, =24, d= 8, and a, = 48.
A:
Q: d dx 1 + 11* 3, x2
A: Given function is e5+1x23+11x
Q: I dx 66. x4 +1
A:
Q: [e³(5e* + 8) 6 dx.
A: see below the answer and calculation
Q: d. √³|x² – 3x − 4|dx - -
A:
Q: Fuid x;on [o,360) 2"(-2)
A:
Q: = 4 . Enter the value of x, where 240 = 4.
A:
Q: /49 — е2 dz – e²
A:
Q: D dx = 4x + C
A:
Q: Prove that
A:
bartleby

Concept explainers

Differential Equations
Have you ever observed the movement of the satellites and rockets or how the planets go around the sun in their orbits? How will you determine their motion? Definitely they follow some scientific laws and these kinds of problems are framed as differentia…
Question
100%
If \(\vec{A} = f(t)\) and \(\vec{B} = f(t)\) are two vectors, find \(\frac{d^2}{dt^2} (\vec{A} + \vec{B})\) at \(t = 1\). [Here you can choose \(\vec{A}\) and \(\vec{B}\) like \(\vec{A} = t^2 \hat{i} - t \hat{j} + (2t + 1) \hat{k}\) & \(\vec{B} = \cos 2t \hat{i} + \sin 3t \hat{j}\) but not similar to these].
expand button
Transcribed Image Text:If \(\vec{A} = f(t)\) and \(\vec{B} = f(t)\) are two vectors, find \(\frac{d^2}{dt^2} (\vec{A} + \vec{B})\) at \(t = 1\). [Here you can choose \(\vec{A}\) and \(\vec{B}\) like \(\vec{A} = t^2 \hat{i} - t \hat{j} + (2t + 1) \hat{k}\) & \(\vec{B} = \cos 2t \hat{i} + \sin 3t \hat{j}\) but not similar to these].
Expert Solution
Check Mark
Step 1

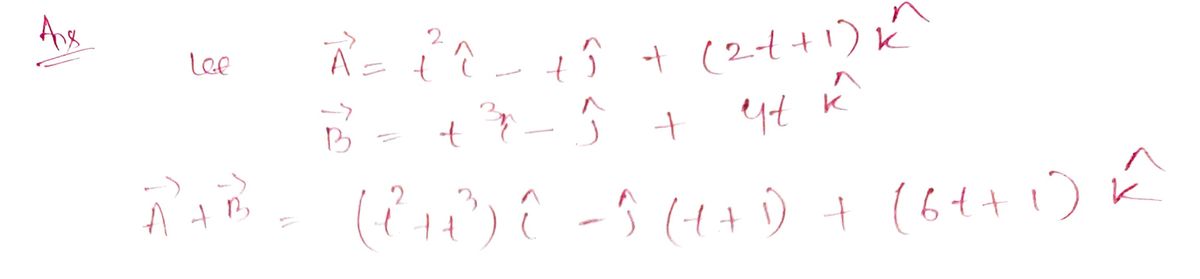
Advanced Math homework question answer, step 1, image 1

bartleby

Step by stepSolved in 2 steps with 2 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Advanced Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS