
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Let the set R(2×2) of 2×2-matrices be a
Let A∈R2×2, (I) be the identity matrix, and x∈R.
Determine whether the following sets are subspaces of R2×2:
(d) {(a b 0 c): a, b, c ∈ R}.
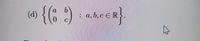
Transcribed Image Text:{(: )
(d)
a, b, c E R
:
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- The set of all 2x2 symmetric matrices is a vector space Select one: O True O Falsearrow_forwardLet W be the subspace of all diagonal matrices in M2.2. Find a basis for W. Then give the dimension of W. If you need to enter a matrix as part of your answer, write each row as a vector. For example, write the matrix ab c d as {(a, b), (c, d)}arrow_forwardIs W a subspace of V? If not, state why. Assume that V has the standard operations. (Select all that apply.) W is the set of all 2 × 2 matrices of the form u 0 0v V = M2,2 W is a subspace of V. O W is not a subspace of V because it is not closed under addition. O W is not a subspace of V because it is not closed under scalar multiplication.arrow_forward
- Let U and V be subspaces of Rn. a) Show that Un V = {√ € R¹ : √ € U and ʊ € V} is a subspace of R". b) Let U = null(A) and V = null(B), where A, B are matrices with n columns. Express UV as either null(C) or im(C) for some matrix C. (You may wish to write C as a block matrix.) c) Let U = null(X) where X has n columns, and V = im(Y), where Y has n rows. Show that if UnV ‡ {0} then XY is not invertible.arrow_forwardGiven an arbitrary m x n matrix M and a vector b0, is the solution set of Mv = b a vector space? Explain.arrow_forwardLet V be a vector space of dimension n, and let B and C be bases for V. Then the product PB- cPc-B is equal to the n × n identity matrix. True Falsearrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

