Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
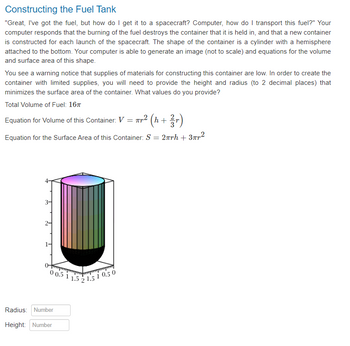
Transcribed Image Text:Constructing the Fuel Tank
"Great, I've got the fuel, but how do I get it to a spacecraft? Computer, how do I transport this fuel?" Your
computer responds that the burning of the fuel destroys the container that it is held in, and that a new container
is constructed for each launch of the spacecraft. The shape of the container is a cylinder with a hemisphere
attached to the bottom. Your computer is able to generate an image (not to scale) and equations for the volume
and surface area of this shape.
You see a warning notice that supplies of materials for constructing this container are low. In order to create the
container with limited supplies, you will need to provide the height and radius (to 2 decimal places) that
minimizes the surface area of the container. What values do you provide?
Total Volume of Fuel: 16T
Equation for Volume of this Container: V = πr² (h+
Equation for the Surface Area of this Container: S = 2πrh+ 3πr²
3-
0 0.5 11.5 2
Radius: Number
Height: Number
1.5 10.50
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 13 images
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
how do you get from start to finsh in the pic pleaseexplain in detail
![To minimize the surface area and differentiate with respect to \( r \):
\[
\frac{d}{dr} S = \frac{d}{dr} \left( \pi \left( \frac{32}{r} + \frac{5}{3} r^2 \right) \right)
\]
\[
\Rightarrow \frac{d}{dr} S = \pi \left( -\frac{32}{r^2} + \frac{10}{3} r \right)
\]
Now, set this value to zero and solve for \( r \):
\[
r = 2.13
\]
Substitute the value of \( r \) back into Step 1 to find:
\[
h = 2.13
\]](https://content.bartleby.com/qna-images/question/f0c2c17c-c864-4c22-95dc-8933004abe78/26086fc6-deba-4040-a0d7-b4f650aaaa8c/714igu_processed.png)
Transcribed Image Text:To minimize the surface area and differentiate with respect to \( r \):
\[
\frac{d}{dr} S = \frac{d}{dr} \left( \pi \left( \frac{32}{r} + \frac{5}{3} r^2 \right) \right)
\]
\[
\Rightarrow \frac{d}{dr} S = \pi \left( -\frac{32}{r^2} + \frac{10}{3} r \right)
\]
Now, set this value to zero and solve for \( r \):
\[
r = 2.13
\]
Substitute the value of \( r \) back into Step 1 to find:
\[
h = 2.13
\]
Solution
by Bartleby Expert
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
how do you get from start to finsh in the pic pleaseexplain in detail
Transcribed Image Text:To minimize the surface area and differentiate with respect to \( r \):
\[
\frac{d}{dr} S = \frac{d}{dr} \left( \pi \left( \frac{32}{r} + \frac{5}{3} r^2 \right) \right)
\]
\[
\Rightarrow \frac{d}{dr} S = \pi \left( -\frac{32}{r^2} + \frac{10}{3} r \right)
\]
Now, set this value to zero and solve for \( r \):
\[
r = 2.13
\]
Substitute the value of \( r \) back into Step 1 to find:
\[
h = 2.13
\]
Solution
by Bartleby Expert
Knowledge Booster
Similar questions
- Can you please help me with thisarrow_forwardCourse Messages Gradebook Home > MT180 Summer 2024 > Assessment Assignment 2.3 Score: 8.67/13 9/13 answered Question 11 An eastbound train and a westbound train meet each other on parallel tracks heading in opposite directions. The eastbound train travels & miles per hour faster than the westbound train. After 2 hours, they are 260 miles apart. At what speeds are the two trains traveling? Write an equation using the information as it is given above that can be used to solve this problem. Use the variable r to represent the speed of the westbound train. Equation: The eastbound train is traveling The westbound train is traveling Question Help: Message instructor Calculator Submit Question mph. mph. útv 24 C NAarrow_forwardassighiment/47 Tassesslient Question 2 2. Here is a balanced hanger diagram. Each triangle weighs 2.5 pounds, each circle weighs 3 pounds, and x represents the weight of each square. Select all equations that represent the hanger. A. x+x+x+x+11=x+ 11.5 B. 2x = 0.5 C. 4x +5+6 = 2x + 2.5 + 6 D. 2x+ 2.5 = 3 E. 4x+2.5 + 2.5 + 3+3 = 2x + 2.5 +3+3+3 DELL 女 Of & %23 4. 6. 8. HHK 00arrow_forward
- Use a graphical method to find the values of x and y that satisfy these simultaneous equations. One of the equations has been plotted. y = -2x + 5 y = x -3 8arrow_forwardSolutionsarrow_forwardses IKL Wite variable IKL Write variabile EXL Wite and so entity equl . xt com/math/algebra 1/wrte-and-solve equations-that represent diagrams BC Bookmarks Maya Paniagua Cl. IXL Search topics and skills Welcom Learning Diagnostic Analytics Recommendations Skill plans AMath FL Standands Algebra 1 >1.2 Write and solve equations that represent diagrams GBC You have prizes to reveal Write an equation that says that the length of the green line is equal to the length of the black line. Combine like terms. Then solve for y. 40 3y 15 Equation: y = DELLarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,