
Structural Analysis
6th Edition
ISBN: 9781337630931
Author: KASSIMALI, Aslam.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Considering the cumulative arrivals and departures of a freeway bottleneck location below, what is the capacity of the bottleneck location
Considering the cumulative arrivals and departures of a freeway bottleneck location below, what is the maximum size of queue that forms?
Considering the cumulative arrivals and departures of a freeway bottleneck location below, what is the longest wait time that any vehicle experiences?
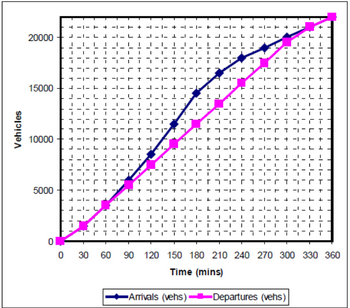
Transcribed Image Text:Vehicles
20000
15000
10000
5000
+--+-|-|- + -1
LL |_ ± _| -
LJ
I
ī
ГТ
r+
++
ГТ
-1-+
JILJ
+
I I
Tī
I
-+---+ -|-
+ --
++--
+--
LIL
I
־ז
IT
+----+-1
LLL
·|-
LJIL
LI
FA
í
Tr
-- +
++ -1
r
−1− 1 −1-T +
_I_ LJ -L
F +-1-1-+-1
+--1--1--1
-|- -| − + + −| − |- + −| − |- + − −|- |- -|- + -|- ++
+
++
0
0 30 60 90 120 150 180 210 240 270 300 330 360
Time (mins)
➡➡Arrivals (vehs)-Departures (vehs)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 6 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Similar questions
- The gate entrance to a park opens at 8:00 AM and there are 18 vehicles in the queue waiting to enter. Vehicles continue to arrive (from 8:00 AM onward) at a constant rate of 8 veh/min. The gate attendant processes vehicles at a constant rate of 1 vehicle every 6 seconds. Assume D/D/1 queuing for the vehicle arrival and departure processes at this gate. What is the average delay per vehicle (min/veh) from 8:00 AM until the queue clears? 0.9 1.1 4.5 9 Ο Ο 81arrow_forwardThe arrival times of vehicles at the ticket gate of a sports stadium may be assumed to be Poisson with a mean of 30 veh/h. It takes an average of 1.5 min for the necessary tickets to be bought for occupants of each car. 6-23 (a) What is the expected length of queue at the ticket gate, not including the vehicle being served? (b) What is the probability that there are no more than 5 cars at the gate, including the vehicle being served? (c) What will be the average waiting time of a vehicle?arrow_forward9- Vehicles arrive at a recreational park booth at a uniform deterministic rate of 4veh/min. If uniform deterministic processing of vehicles (collecting of fees) begins 30 minutes after the first arrival and the total delay is 3600 veh-min, how long after the arrival of the first vehicle will it take for the queue to be cleared?arrow_forward
- 7. Queue Theory: At the end of a sporting event, vehicles begin leaving a parking lot at 2(1) = 12 - 0.25t and vehicles are processed at u(t) = 2.5 + 0.5t (t is in minutes and 2(t) and u(t) are in vehicles per minute). Assume D/D/1 determine: Time when queue clears and total vehicle delay.arrow_forwardA)An intersection approach has a capacity of 1600 vph. What is the likely queue at the end of an hour if the 15 minute vehicle arrivals are 350, 500, 300, and 500? B) What is the cumulative lost time per hour if the lost time per phase is 4 seconds and the intersection operates as a 4 phase 120 second cycle? C) A queue of 200 veh. is built up waiting to get into a national park prior to open. How long it will take to clear the queue if each vehicle takes 15 seconds, yet veh. continue to arrive at 60 vph? D) The allocated effective green time across 3 phases if critical volumes are 300, 200 and 100 vehicles respectively if you have a 75 second cycle. Assume Y+AR = tl = 5 sec/ phase. E) A roadway has an estimated density of 50 vpmpl. What percent of time is a highway detector covered if the detector is 5 ft long? Assume 28 ft veh length.arrow_forwardAt time ? = 0, when the border inspection station was scheduled to open, eight vehicles were already waiting in a queue in front of an inspection booth. Vehicles continued to arrive at a rate of 4 veh/minute. The officer did not start the inspection until ? = 4 minutes. When ?≥4 minutes, the barrier was lifted and vehicles left at a rate of 7.5 veh/minute. Draw the vehicle arrival and departure curves in the following graph. From the graph, determine the maximum queue length and the time the queue disappears. Assume D/D/1 queuing.arrow_forward
- There is a single gate at an entrance to a recreational park where arriving vehicles must stop to pay their tickets. The park opens at 8:00AM, at which time vehicles begin to arrive at a rate of 480 veh/hr. After 20 minutes the arrival flow rate declines to 120 veh/hr, and it continues at that level for the remainder of the day. If the service time is 15 seconds per vehicle, and assuming D/D/1 queuing, determine the Length of Queue at 8:1OAM. Note: Round off your answers to the nearest whole number. Only include the numeric value of your answer without the unit (i.e. 22).arrow_forwardehicles arrive at a single toll booth beginning at 8:00 A.M. They arrive and depart according to a uniform deterministic distribution. However, the toll booth does not open until 8:10 A.M. The average arrival rate is 8 veh/min and the average departure rate is 10 veh/min. Assuming D/D/1 queuing, when does the initial queue clear and what are the total delay, the average delay per vehicle, longest queue length (in vehicles), and the wait time of the 100th vehicle to arrive (assuming first-in-first- out)?arrow_forwardvehicles start to arrive at a parking area at 6 am with an arrival rate function(vehicles per minute) of lambda(t)=1.2+(0.3)t, where t is in minutes. At 6:15 am, the parking area opens and processed vehicles at a rate of 12 per minute. a)Determine when does the queue clear? b)find the total delay? c)find the maximum queue length?arrow_forward
- Vehicle arrivals in an event are assumed Poisson distributed with an average arrival rate of (15.4) vehicles in every 2 minutes. What is the probability of the following: a. Exactly 14 vehicles arrive in a 2.5-minute interval. b. Less than 14 vehicles arrive in a 2.5-minute interval. c. More than 14 vehicles arrive in a 2.5-minute interval.arrow_forwardA student records the number of vehicles that pass through a toll road lane, as shown in the following list Calculate: (c) what is the busiest flow rate for a 15-minute period in this lane?arrow_forwardVehicles leave an airport parking facility (arrive at parking fee collection booths) at a rate of 400 veh/h (the time between arrivals is exponentially distributed). The parking facility has a policy that the average time a patron spends in a queue waiting to pay for parking is not to exceed 3 seconds. If the time required to pay for parking is exponentially distributed with a mean of 12 seconds, what is the smallest number of payment processing booths that must be open to keep the average time spent in a queue below 3 seconds?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning


Structural Analysis (10th Edition)
Civil Engineering
ISBN:9780134610672
Author:Russell C. Hibbeler
Publisher:PEARSON

Principles of Foundation Engineering (MindTap Cou...
Civil Engineering
ISBN:9781337705028
Author:Braja M. Das, Nagaratnam Sivakugan
Publisher:Cengage Learning

Fundamentals of Structural Analysis
Civil Engineering
ISBN:9780073398006
Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel Lanning
Publisher:McGraw-Hill Education


Traffic and Highway Engineering
Civil Engineering
ISBN:9781305156241
Author:Garber, Nicholas J.
Publisher:Cengage Learning