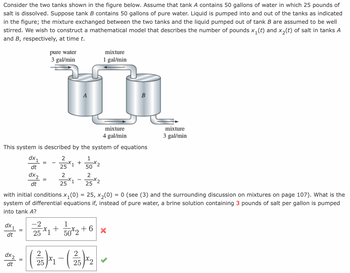
Consider the two tanks shown in the figure below. Assume that tank A contains 50 gallons of water in which 25 pounds ofsalt is dissolved. Suppose tank B contains 50 gallons of pure water. Liquid is pumped into and out of the tanks as indicatedin the figure; the mixture exchanged between the two tanks and the liquid pumped out of tank B are assumed to be wellstirred. We wish to construct a mathematical model that describes the number of pounds x₁(t) and x₂(t) of salt in tanks Aand B, respectively, at time t.dx₁1dtdx1dtpure water3 gal/minmixture4 gal/minThis system is described by the system of equations150225dx2dt225225*11+-X2mixture1 gal/min-X2Bwith initial conditions x₁(0) = 25, x₂(0) = 0 (see (3) and the surrounding discussion on mixtures on page 107). What is thesystem of differential equations if, instead of pure water, a brine solution containing 3 pounds of salt per gallon is pumpedinto tank A?-225*1 + 50x2+6×dx22 - (25)*₁- (25)×₂2 -=x2dtmixture3 gal/min

Answered: Image /qna-images/answer/d139643e-dd22-45c0-974a-1315fd1f2591.jpg

Answered: Consider the two tanks shown in the…

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

Answer this question correctly along with the correct answer.
Given the description of the phenomena, identify the corresponding mathematical model. A population of fish P(t) lives in an environment with limited resources. As a result, the environment can only support the population if it contains no more than 100, 000 fish (otherwise some fish would starve due to an inadequate supply of food). At any given time, the relative number of additional fish the environment can support is (100, 000 · by 100, 000. Due to the environment, the population grows at a rate proportional to the product of the current P) divided population and the relative number of additional fish the environment can support. dP kP(100,000 – P) a. %D dt 100,000 k(100, 000 – P) b. dP %3D dt 100, 000 C. dP = k(100, 000 – P) dt O d. dP kP %3D dt 100, 000
a-)Answer the question in the picture. b-)Approximate the value of the root of f(x)=e-x(3.2sin(x)-0.5cos(x)) using the bisection method to within 0.01 of its actual value. c-) The current population of Ankara is 4,650,000 in 2010. Write a linear equation if the population increases by 3% each year
An iron rod 10 m long is attached to end A with a constant temperature of 100⁰ Celsius, while at end B the temperature is maintained at 0⁰ C. The initial temperature along the length of the rod is 0⁰ C. This temperature will propagate along the rod from A to B, which can be described in the form of an equation following. (Image) Calculate the temperature along the length of the rod using an explicit scheme. Use Δt = 2m and Δt = 10 sec and K = 1m²/s. The count is carried out until the second time
The chemical processes in your body are facilitated by enzymes which determine the rate at which different reaction occurs. The rate of a chemical reaction v is determined by the Michaelis-Menten equation. For example consider the following reaction breaking down a substrate S into two particles P1 and P2. The Michaelis-Menten equation tells us that the rate of the reaction is: v = aS/ b+S . Question 1: Plot v if a = 0.14 and b = 0.015 for a domain of S ∈ [0, 0.5] (See attached image for diagram!) Question 2: How do we find the horizontal asymptote? (multiple choice, choose one below) A. limS→0 v(S) B. limS→∞ v(S)
3.3-2
Fresh water flows into tank 1; mixed brine flows from tank 1 into tank 2, from tank 2 into tank 3, and out of tank 3; all at the given flow rater gallons per minute. The initial amounts x₁(0)=xo (lb), and x₂(0) = 0, and x3 (0) = 0 of salt in the three tanks are given, as are their volumes V₁, V₂, and V3. First solve for the amounts of salt in the three tanks at time t, then determine the maximal amount of salt that tank 3 ever contains. Finally, construct a figure showing the graphs of x₁ (t), x₂ (t), and x3 (t). r=60, x=60, V₁ = 15, V₂ = 12, V3 = 20 X₁ (t) = X₂ (t) = X3 (t)=
(3) The approximate enrollment, in millions between the years 2009 and 2018 is provided by a linear model Y3D0.2309x+18.35 Where x-0 corresponds to 2009, x=1 to 2010, and so on, and y is in millions of students. Use the model determine projected enrollment for the year 2014. 近

The following problem deals with the open three-tank system. Fresh water flows into tank 1; mixed brine flows from tank 1 into tank 2, from tank 2 into tank 3, and out of tank 3; all at the given flow rate r gallons per minute. The initial amounts x1(0)= x0 (lb), x2(0) = 0, and x3(0) = 0 of salt in the three tanks are given, as are their volumes V1, V2, and V3 (in gallons). First solve for the amounts of salt in the three tanks at time t , then determine the maximal amount of salt that tank 3 ever contains. Finally, construct a figure showing the graphs of x1 (t) , x2(t) , and x3(t) r = 60, x0 = 45, V1 = 15, V2 = 10, V3 =30
You have measured the water level of a reservoir at different times throughout an year. You need to find the minimum water level that the reservoir had in that year based on these measurements. To work this out which numerical methods would you need and which order would you need to apply them in? O a. Solving a system of linear equations followed by solving an ODE. b. Curve fitting, followed by solving an ODE. c. Solving an ODE followed by root-finding applied to the derivative of the resultant curve. Od. Root finding followed by numerical integration. e. Numerical integration followed by solving a system of linear equations. O f. Curve fitting, followed by numerical integration. O g. Curve fitting followed by root-finding applied to the derivative of the fitted curve. Oh. Numerical integration followed by solving an ODE. UND DND OXO
4. Find the first three nonzero terms in each of two linearly independent solutions of the equation. (1+x²)y" + xy = 0
In 1992, the moose population in a park was measured to be 3790. By 1999, the population was measured again to be 3440. If the population continues to change linearly: A.) Find a formula for the moose population, P, in terms of t, the years since 1990. P(t) = B.) What does your model predict the moose population to be in 2009?

SEE MORE QUESTIONS

Recommended textbooks for you

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Advanced Engineering Mathematics

Advanced Math

ISBN:

9780470458365

Author:

Erwin Kreyszig

Publisher:

Wiley, John & Sons, Incorporated

Numerical Methods for Engineers

Advanced Math

ISBN:

9780073397924

Author:

Steven C. Chapra Dr., Raymond P. Canale

Publisher:

McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…

Advanced Math

ISBN:

9781118141809

Author:

Nathan Klingbeil

Publisher:

WILEY

Mathematics For Machine Technology

Advanced Math

ISBN:

9781337798310

Author:

Peterson, John.

Publisher:

Cengage Learning,

Basic Technical Mathematics

Advanced Math

ISBN:

9780134437705

Author:

Washington

Publisher:

PEARSON

Topology

Advanced Math

ISBN:

9780134689517

Author:

Munkres, James R.

Publisher:

Pearson,

SEE MORE TEXTBOOKS