ENGR.ECONOMIC ANALYSIS
14th Edition
ISBN: 9780190931919
Author: NEWNAN
Publisher: Oxford University Press
expand_more
expand_more
format_list_bulleted
Related questions
Question
Consider the two-period Real Business Cycle (RBC) model without uncertainty presented in the lecture slides, but with one modification. Now assume that the instantaneous utility function for households takes the form:
where Ct is consumption at time t and (1- lt) is leisure time at time t. Given that the time endowment is normalized to 1, it follows that lt is hours worked at time t. Finally, Ɵ > 0, b > 0 and gamma > 0 are parameters.
All households in the economy are assumed to be identical. We can therefore consider a 'representative household' (henceforth 'the household'). Set t = 1 for the present period and set t = 2 for the next period. For example, C1 is consumption in the present period and C2 is consumption in the next period. Remember, this is a two-period model so there are no time periods prior to t = 1 and there are no time periods after t = 2 Assume that the household begins and ends life with no accumulated wealth and that the real interest rate is r (where r>0).
a) Present the Lagrangian (constrained maximization) problem for the household under this modified specification.
b) Derive the first order conditions for the household in this case. [Hint: the household chooses C1, C2, L1 and L2].
Transcribed Image Text:1-e
U: =
(I – 1,)1-y
+ b
1-0
1-Y
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
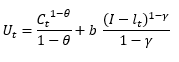
Step by stepSolved in 4 steps with 9 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, economics and related others by exploring similar questions and additional content below.Similar questions
- N⁵q1arrow_forwardConsider the two-period Real Business Cycle (RBC) model without uncertainty presented in the lecture slides, but with one modification. Now assume that the instantaneous utility function for households takes the form: where Ct is consumption at time t and (1- lt) is leisure time at time t. Given that the time endowment is normalized to 1, it follows that lt is hours worked at time t. Finally, Ɵ > 0, b > 0 and gamma > 0 are parameters. All households in the economy are assumed to be identical. We can therefore consider a 'representative household' (henceforth 'the household'). Set t = 1 for the present period and set t = 2 for the next period. For example, C1 is consumption in the present period and C2 is consumption in the next period. Remember, this is a two-period model so there are no time periods prior to t = 1 and there are no time periods after t = 2 Assume that the household begins and ends life with no accumulated wealth and that the real interest rate is r (where…arrow_forwardAssume you can work as many hours you wish at £12 per hour (net of tax). If you do not work, you have no income. You have no ability to borrow or lend, so your consumption, c, is simply equal to your income. Derive and plot the feasible set, between daily values of consumption c, and “leisure”, l. Label the values at the intercepts (the points where the feasible frontier cuts the two axes).arrow_forward
- Consider a two-period model in which the goverment introduces a tax on interest earnings. This means that borrowers pay a net interest rate of r, however lenders (savers) receive a net interest rate of (1 – t)r on their savings, where t is the tax rate withheld by the government and is a multiplication sign. Let r = 8 percent and t = 28 percent. Consider a consumer who is a saver. Answer parts a), b), c) and d) below. Round your numerical answer in part a) to 3 decimal places. a). The relative price of consumption today to consumption tomorrow for this saver is b). Suppose the tax rate increases. How does the saver's relative price of consumption today change? A. Consumption today has the same price relative to consumption tomorrow. B. Consumption today becomes relatively more expensive C. Consumption today becomes relatively cheaper c). As a result, the substitution effect shows that A. Consumption today increases, while consumption tomorrow decreases B. Consumption today remains…arrow_forward1. Consider an individual with quasi hyperbolic discounting, the (8,6) model, who lives over three periods, t= 1,2,3. Let e denote consumption in period t = 1,2,3. Assume that the per-period utility function is given by the natural logarithm function, for c>0, u (c₂) = Inc. There is a labor income y> 0 in period 1 but no income in subsequent periods. We assume for now that the individual can only save in one period financial instruments with its interest rate being normalized to be zero. (1) Write down the lifetime discounted utilities of self 1 and self 2 and the budget constraints in each time period. Suppose that 3= 1 and 6 = 1 in (2), (3), and (4). (2) Derive the optimal consumption/saving behavior of self 2, given a strictly positive saving in period 1, 81 > 0. (3) Derive the optimal consumption/saving behavior of self 1, anticipating the optimal behavior of self 2. (4) Suppose that the individual in period 1, self 1, can commit a consumption plan that is binding to self 2. Derive…arrow_forwardPlease see attached: Answer does not require any explanation. Feel free to just state answer.arrow_forward
- Consider the following one-period model. Consumer Utility function over consumption (C) and leisure (L) U(C,L)= C^(1/2)L^(1/2) = Total hours: H = 40 Labour hours: = H – L Non-labour income: π Lump-sum tax: T Hourly wage: w Firm Production function: Y = zF() = z Total factor productivitiy: z = 2 Government Government spending (exogenous): G = 20 Suppose that the total factor productivity, z, increases to 5. What is the substitution effect of this wage change on labour supply()? A. +8.51 B. -5.51 C. -8.51 D. +5.51 E. None of the abovearrow_forwardQuestion 3: Consider the two-period model. The consumer has an asset, which is worth A in the current period. The current and future incomes are y and y'. There are no taxes. The maximum amount that the consumer can borrow in the current period is A. The market interest rate is r and the consumer's asset will be worth (1 + r) A in the future period. The consumer's indifference curves are linear with slope steeper than 1+r. 1. Illustrate the consumer's budget constraint and equilibrium in a graph with current consumption (c) on x axis and future consumption (c') on y axis. Clearly mark the consumer's endowment point (y, y'). 2 2. Suppose the current-period value of the consumer's asset doubles to 2A. Illustrate the consumer's new budget constraint and equilibrium in the same graph. Explain your answer.arrow_forwardConsider the following 2-period model U(C1,C2) = min{3C1,4C2} C1 + S = Y1 – T1 C2 = Y2 – T2 + (1+r)S Where C1 : first period consumption C2 : second period consumption S : first period saving Y1 = 20 : first period income T1 = 5 : first period lump-sum tax Y2 = 50 : second period income T2 = 10 : second period lump-sum tax r = 0.05 : real interest rate Find the optimal saving, S*arrow_forward
- What conditions must non-linear time series models, such as vector autoregressive models, satisfy in order to use impulse response functionsarrow_forwardHello! please can you solve question B? Thanksarrow_forwardConsider the two-period household-maximization model discussed in class. The model is modified in order to look at applications including credit constraints, interest-rate markups, and taxation. A representative household lives for two periods and maximizes utility of consumption in period 1 and in period 2. The utility is represented by log(c) where c denotes consumption. Assuming no discounting between period 1 and period 2. The maximization problem for the representative household can be written as a) Explain what is meant by a representative household. Briefly explain the budget constraints of the representative households and of the government. Explain the role played by the assumption that the representative households lives for only two periods and the assumption of “no discounting”.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Principles of Economics (12th Edition)EconomicsISBN:9780134078779Author:Karl E. Case, Ray C. Fair, Sharon E. OsterPublisher:PEARSON
Engineering Economy (17th Edition)EconomicsISBN:9780134870069Author:William G. Sullivan, Elin M. Wicks, C. Patrick KoellingPublisher:PEARSON
Principles of Economics (MindTap Course List)EconomicsISBN:9781305585126Author:N. Gregory MankiwPublisher:Cengage Learning
Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning
Managerial Economics & Business Strategy (Mcgraw-...EconomicsISBN:9781259290619Author:Michael Baye, Jeff PrincePublisher:McGraw-Hill Education
Principles of Economics (12th Edition)
Economics
ISBN:9780134078779
Author:Karl E. Case, Ray C. Fair, Sharon E. Oster
Publisher:PEARSON
Engineering Economy (17th Edition)
Economics
ISBN:9780134870069
Author:William G. Sullivan, Elin M. Wicks, C. Patrick Koelling
Publisher:PEARSON
Principles of Economics (MindTap Course List)
Economics
ISBN:9781305585126
Author:N. Gregory Mankiw
Publisher:Cengage Learning
Managerial Economics: A Problem Solving Approach
Economics
ISBN:9781337106665
Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike Shor
Publisher:Cengage Learning
Managerial Economics & Business Strategy (Mcgraw-...
Economics
ISBN:9781259290619
Author:Michael Baye, Jeff Prince
Publisher:McGraw-Hill Education