Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: Diagonalize matrix A, i.e., find diagonal D and invertible P such that A = PDP-1, where -[:] 3 2 A =…
A:
Q: If A is an nxn invertible matrix, then det(A-1) is equal to O det (A)-"det(adj(A)) O None of these…
A:
Q: Exercise: Consider x = (3-2) fundamental (a) Find a matrix. YLt).
A: Find Eigenvalues Eigenvectors corresponding to eigenvalues.
Q: Let B=(b₁,b₂), C=(C₁,C₂), be bases for R² b₁ = (-5,-3), b₂ =(3,2), C₁=(1,3), C₂ = (1,2) Find the…
A:
Q: Suppose A is a symmetric matrix. (Au)" : u"A
A:
Q: Let 3 A = -1 -1 3 -1 -1 3 (a) Find a matrix P that orthogonally diagonalizes A. (b) Find B = P-¹AP…
A:
Q: Let A = (a) Find a matrix P that orthogonally diagonalizes A. (b) Find B = P-¹AP using the (correct)…
A: Given: A matrix A=2-1-1-12-1-1-12 To find:  a matrix P that orthogonally diagonalizes A. B=P-1AP
Q: Example. 2 -5 Consider x² = ( ² =_=_=) * -2 (a) Find a fundamental matrix. (/(t). (b) Find the…
A:
Q: -1 3 -12 0 5 -2 -1 ^- |- Determine whether A is diagonalizable. late (4)10 If A is diagonalizable,…
A:
Q: -1 Suppose A, B, C, X are invertible n x n matrices. Solve the matrix equation C(B1X) = (B-²C-1) B²…
A: If A and B are nxn invertiable matrices then(AB)-1=B-1A-1
Question
2. Consider the system \[ \vec{x}' = \begin{pmatrix} 2 & -5 \\ 1 & -2 \end{pmatrix} \vec{x}. \] (a) Find a fundamental matrix \( \Psi(t) \). (b) Find the special fundamental matrix \( \Phi(t) \) so that \( \Phi(0) = I \).
expand button
Transcribed Image Text:2. Consider the system \[ \vec{x}' = \begin{pmatrix} 2 & -5 \\ 1 & -2 \end{pmatrix} \vec{x}. \] (a) Find a fundamental matrix \( \Psi(t) \). (b) Find the special fundamental matrix \( \Phi(t) \) so that \( \Phi(0) = I \).
Expert Solution
Check Mark
Step 1

NOTE: According to guideline answer of first question can be given, for other please ask in a different question and specify the question number .

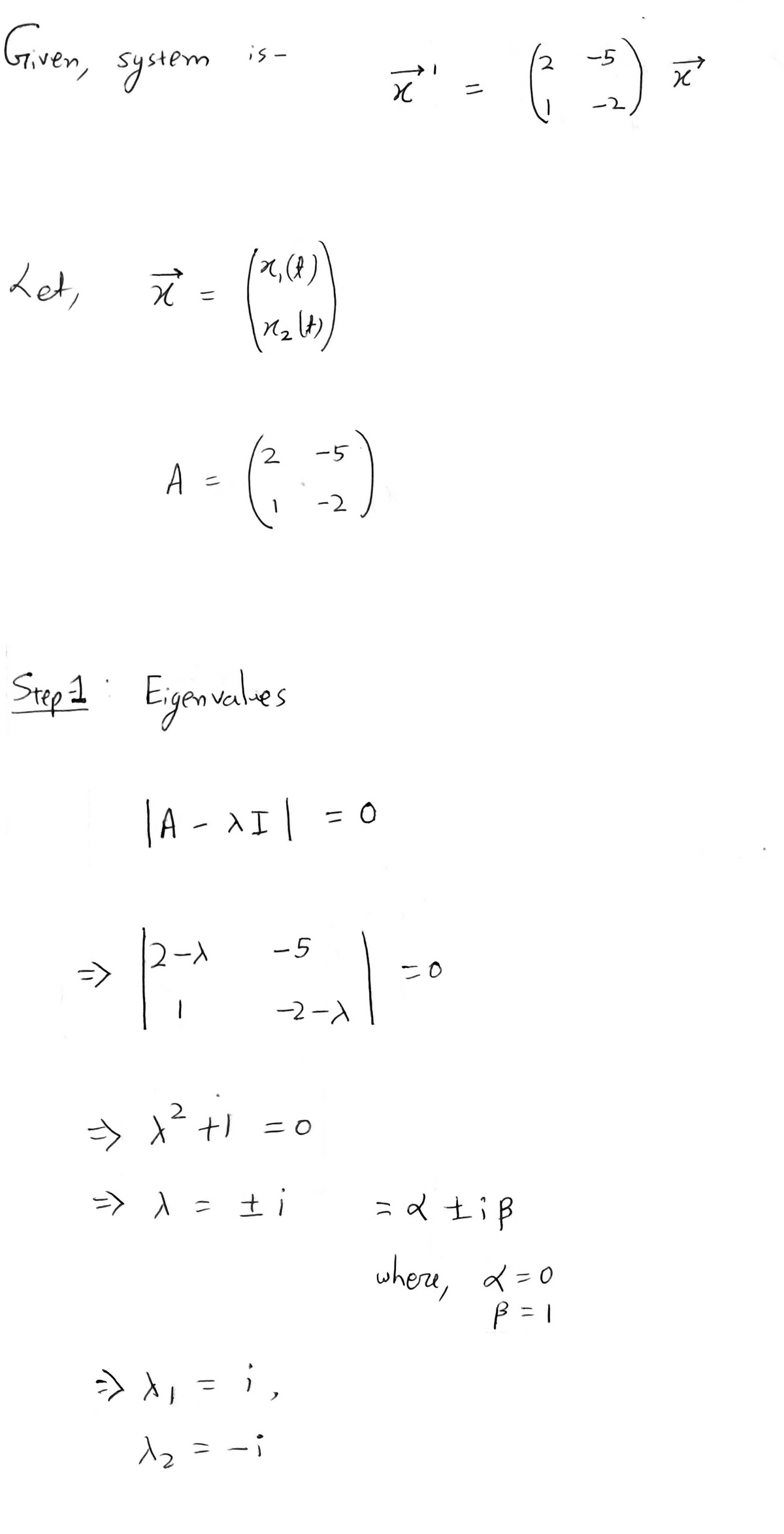
Advanced Math homework question answer, step 1, image 1

Step 2

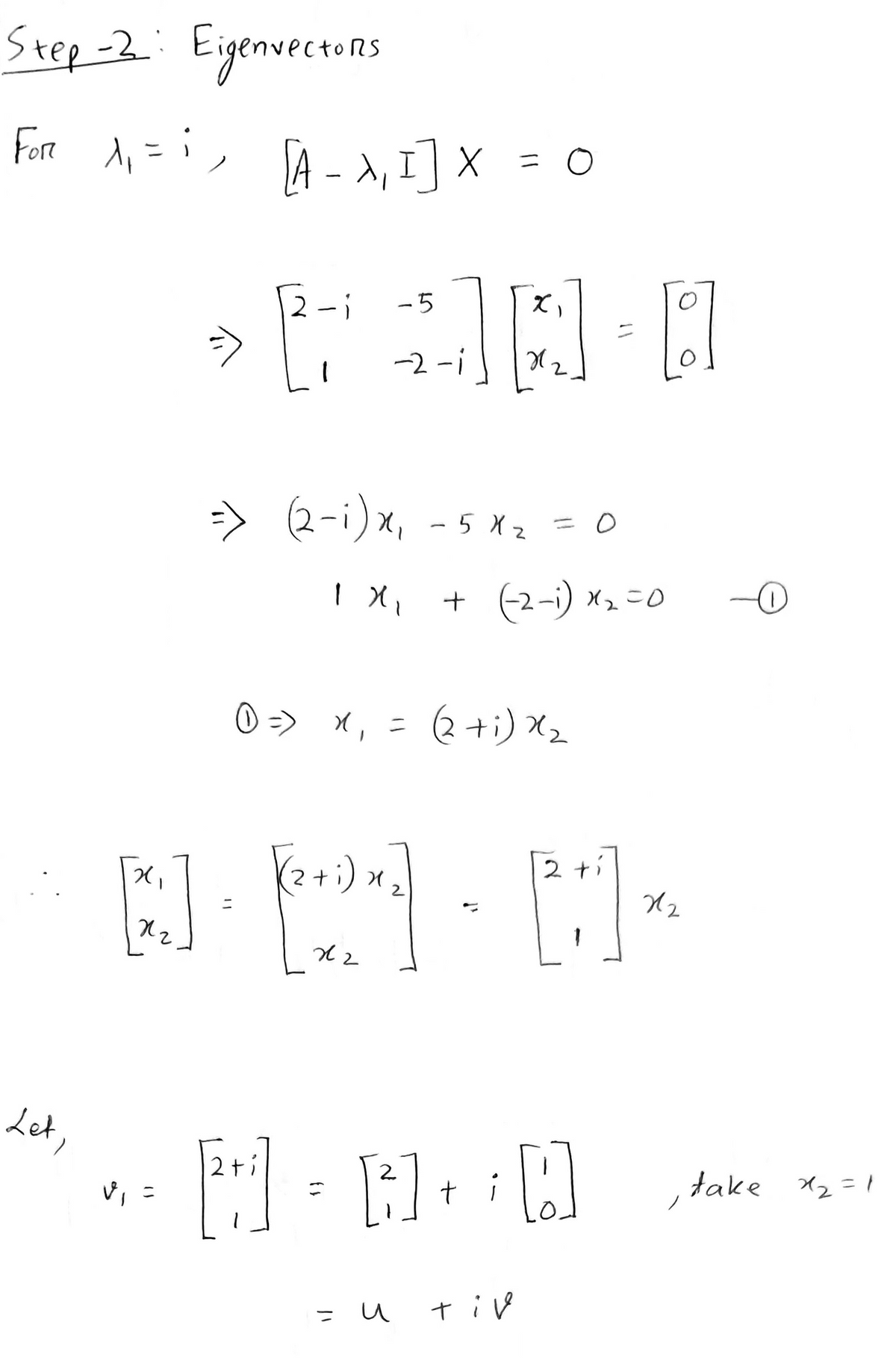
Advanced Math homework question answer, step 2, image 1

 

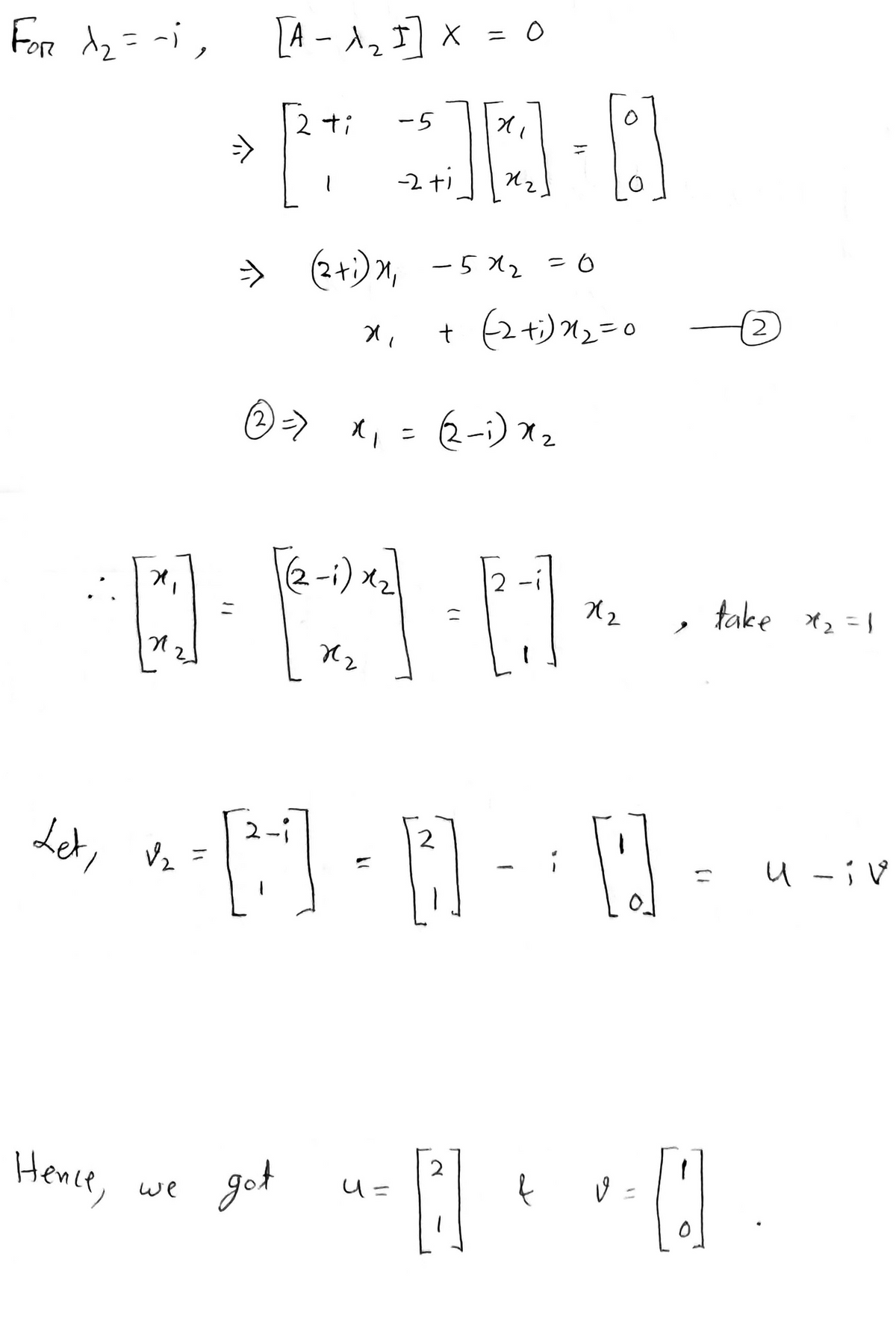
Advanced Math homework question answer, step 2, image 2

bartleby

Step by stepSolved in 3 steps with 4 images

Blurred answer
Knowledge Booster
Background pattern image
Advanced Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS