Question
Consider the solutions y1 (x, t) = A cos (kx − ωt) and y2 (x, t) = A sin (kx − ωt) . Show that the sum of these wave functions
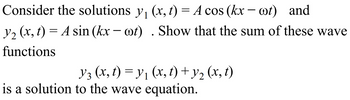
Transcribed Image Text:Consider the solutions y₁ (x, t) = A cos(kx-ot) and
y₂ (x, t) = A sin(kx-ot). Show that the sum of these wave
functions
Y3 (x, t) = y₁ (x, t) + y₂ (x, t)
is a solution to the wave equation.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- The question is in the image I submittedarrow_forward(WF-3) Consider the two normalized wave function shown below. Calculate the expectation value for position. y(x) = √√3(1 + ix)/2 for 0 ≤ x ≤ 1 and zero everywhere elsearrow_forwardU = U, %3D U = 0 X = 0 A potential step U(x) is defined by U(x) = 0 for x 0 If an electron beam of energy E > U, is approaching from the left, write the form of the wave function in region I (x 0) in terms of the electron mass m, energy E, and potential energy U,. Do not bother to determine the constant coefficients. Formulas.pdf (Click here-->) Edit Vicw Insert Format Tools Table 12pt v Paragraph BIU Av eu T? varrow_forward
- Consider a particle described by the following wavefunction for all values of ™: 0 (t, x) - N exp{-10²²) exp{-1 wt} ar²} = where a = mw/h, and where m, N and w are constants. Now do the following: a) Determine the energy of this particle, E.arrow_forwardIn a certain region of space, a particle is described by the wave function (x) = Cxe-bx where C and b are real con- stants. By substituting into the Schrödinger equation, find the potential energy in this region and also find the energy of the particle. (Hint: Your solution must give an energy that is a constant everywhere in this region, independent of x.)arrow_forwardThe normalization constant of the wavefunction is sqrt(pi)/2aarrow_forward
- Calculate (p) and (p) for the wavefunction, /2 Y (x)={( IT X sin L 0 Larrow_forwardConsider a periodic signal x(t) with period T defined as follows: T x(t) = (5t, -< t <0 (10, 0arrow_forwardA resonator is formed by a convex mirror of radius R1=-1 m and a concave mirror of radius R2=1.5 m. What is the maximum possible mirror separation if this is to remain a stable resonator?arrow_forward
- Consider the wavefunction Vmi (0) emiø (4.5) with my an integer and o < ø< 2n. Find the normalization factor for this wavefunction. Answer, N = (27)-1/2.arrow_forwardsin kx 2) Consider the wavefunction is given y(x) =2N For what value of N х will it be normalized? Hint: a useful integral is (sin dt 3) Prove thatarrow_forwardThe particle is confined to a one-dimensional box between x=0 and x=2. Its wave function is A(x)=6x2/N (0≤x≤1) and A(x)=6/N (1<x≤2), where N is a normalization constant. Calculate the constant N and the average position of the particles.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios