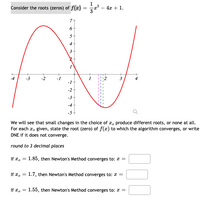
Consider the roots (zeros) of f(x) = a³ – 4x + 1. 7+ 6 5 3 -4 -3 -2 -1 3 -1 -2 - -3 - -4 -5- We will see that small changes in the choice of r, produce different roots, or none at al For each r. given, state the root (zero) of f(x) to which the algorithm converges, or w DNE if it does not converge. round to 3 decimal places If x, = 1.85, then Newton's Method converges to: # = If x, = 1.7, then Newton's Method converges to: æ = If x, = 1.55, then Newton's Method converges to: x = 2.

In the beginning of step 2 it says "Now,as, there always exists constant polynomial over Z" I got feedback underlining the whole line and 'see above' written next to it. How can I fix this?

In each of the following boxes, write the numerical value of the corresponding term of sequence {ak}k≥o whose generating function is a2 az = || a4 = Determine the coefficient of x²2 in the multinomial theorem expansion of (1+x² + x¹ + x6)5. O None of these. 11 x³-1 (1,0,1,3) + (0,2,0,3) + (0,1,2,2) + (0,0,4,1) (1,0,1,3) + (0,2,0,3) + (0,1,2,2) 5 O (1,0,1,3)+(0,2,0,3) + (0.12.2) + (0,1,3,1) (1,0,1,3) + (0,2,0,3) + (0,1,2,2) + (0,0,4,1) + (0,1,3,1)

The Intermediate Value Theorem can be used to approximate a root. The following is an example of binary search in computer science. Suppose you want to approximate /8. You know that it is between 2 and 3. If you consider the function f(x) = a? – 8, then note that f(2) 0. Therefore by the Intermediate Value Theorem, there is a value, 2 < c < 3 such that f(c) = 0. Next choose the midpoint of these two values, 2.5, which is guaranteed to be within 0.5 of the acutal root. f(2.5) will either be less than 0 or greater than 0. You can use the Intermediate Value Theorem again replacing 2.5 with the previous endpoint that has the same sign as 2.5. Continuing this process gives a sequence of approximations rn with T1 = 2.5. How many iterations must you do in order to be within 0.00390625 of the root?