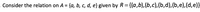
Consider the relation on A = {a, b, c, d, e} given by R={(a,b),(b,c), (b,d),(b,e),(d,

Let X = {a, b, c, d, e,f} and S be the relation on X defined by S = || {(а, а), (а, b), (а, с), (а, d), (а, е), (а, , (b, b), (b, d), (b, е), (b,), (с, с), (с, d), (c, e), (c,f), (d,d), (d, e), (d,f), (e, e), (f,f)}. Is S a partial order? If so, draw its Hasse diagram. If not, give an example showing why.

Consider the relation R = {(1, 2), (1, 4), (2, 3), (3, 1), (4, 2)} on the set {1, 2, 3, 4}. What is the transitive closure of R? O {(1, 2), (1, 4), (2, 3), (3, 1), (4, 2), (1,3), (2,1). (3, 2), (3, 4), (4,3)} O {(1.3), (2,1), (3, 2), (3, 4), (4,3), (1, 1), (2, 2). (2, 4), (3, 3), (4, 1), (4, 4)} O {(1, 2), (1, 4), (2, 3), (3,1), (4,2), (1,3), (2,1), (3, 2), (3, 4). (4, 3), (1, 1). (2, 2), (2, 4), (3. 3). (4, 1). (4, 4)} O {(1,3), (2,1). (3, 2), (3, 4), (4,3), (1, 1), (2, 2), (2, 4), (3, 3), (4, 1), (4, 4)}

Represent the following relation {1,2, 3, 4} with a matrix. {(1,1), (1, 4), (2, 2), (3, 3), (4, 1)}

How many relations are there on the set {a, b}. Show all possible relations on the set {a, b} in matrix format.

v = (5, 2, 4) w = (8, 2, 3) Find the cosine of the angle between v and w. cos 0 =

9.25. Let A = {1, 2, 3, 4, 5, 6}. The relation R = {(1,1), (1, 5), (2, 2), (2, 3), (2, 6), (3, 2), (3, 3), (3, 6), (4, 4), (5, 1), (5, 5), (6, 2), (6, 3), (6, 6)} is an equivalence relation on A. Determine the distinct equivalence classes.

Let A = (0,1,2,3). The relations R, S and T in the set A are defined as follows…R={(0,0),(0,1),(0,3),(1,0),(1,1),(1,3),(2,2),(3,0),(3,1),(3,3)}S ={(0,0),(0,2),(0,3),(2,3)}T={(0,1),(2,3)}Find the equivalent relation is:

Let A = {a, b, c, d} and let R = {(a, a), (a, b), (a, c), (a, d), (b, b), (b, c), (b, d), (c, c), (c, d), (d, d)} be arelation on A. Which of the properties reflexive, symmetric and transitive does the relation R possess? If Rdoes not possess one of these properties, explain why. How do I know where to stop? How do I know when I have proven transitivity? for example? I have difficulties with knowing if my prove is complete or not

For (a,b),(c,d) E N×N define the relation (a,b) ~ (b,c) if and only if ab = cd. Is this relation symmetric and transitive? True False