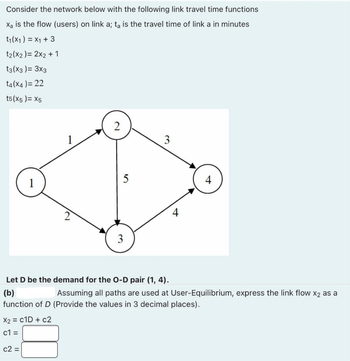
Consider the network below with the following link travel time functions Xa is the flow (users) on link a; ta is the travel time of link a in minutes t₁(x1) = x₁ + 3 t₂(x2) = 2x2 + 1 t3(x3) = 3x3 t4(x4) = 22 t5(x5)= X5 1 2 X2 = C1D + c2 c1= c2= 5 3 3 4 Let D be the demand for the O-D pair (1, 4). (b) Assuming all paths are used at User-Equilibrium, express the link flow X2 as a function of D (Provide the values in 3 decimal places).

Q: If a biker travels 33 miles in 3 hours, can you guarantee that the bike's speedometer must have read…

A: The  main mathematical concept of this problem is the concept of averages. The average is the value…

Q: Consider the map ƒ : [0, 1] → [0, 1] given by x+1/2 0≤ x ≤ 1/2 2 - 2x 1/2 ≤ x ≤ 1 f(x) = { (a) Show…

A:

Q: Prove or disprove Z[√2] = {a+b√2 a, b € Z} is a subring of R[√2] = {a+b√2: a, b = R} :

A: Here, we use definition of subring. To prove our result, we show that,  Z[√2]  is  i) Closed under…

Q: Bisection method 1. Find one real root of 700 g(x) = √(1-e 7) = 185 between 22 to 25 accurate to 4…

A:

Q: Give two function f(x) and f(x) such that the f''x is equal to -2.

A:

Q: Determine the two-variable function F(x, y) if Fy (x, y) = y sin(xy) + x given that x^2 + πχ2 F(x₁ -…

A: Given That: Partial derivative of a function with respect to y is Fy(x,y)=ysin(πxy)+x with the…

Q: Simplify the expression below. Show at least 3 steps, 3² (4-3)³ 20- + 4x (6-2) (12÷4+2) × 2

A:

Q: Given two planes 3x+5y-z = 1 and 4x-y+z =7 and a point P(8,2,0), find a point that belong to the…

A:

Q: dy The following differential equation is separable as it is of the form dx dy - (y 9)² dx = 0 Find…

A: Given differential equation is dy-y-92dx=0⇒dydx=y-92                                ...(1) If we…

Q: Let f be a function from R to R. Without using words of negation, write the meaning of “f is not an…

A: What is Statement: Any style of reasoning starts with a mathematical assertion. A mathematical…

Q: Let p= (P1, P2, P3, P4, P5) be the projection of vector v = (167, 0, 0, 0, 0) on the vector space V.…

A:

Q: M₂=•fc'•b•d² w. (1-0.59 w) 200-10% =0.9.20.7-300-480² w (1-0.59 w)

A: Sol:- Letf(w)=0.9⋅20.7⋅300⋅4802⋅w(1-0.59w)-200⋅106Using Fixed Point Iteration methodHere…

Q: 40

A:

Q: Given the Fourier Cosine Transform: ƒc (w) = √(a²4²), use integration to find the Inverse Fourier…

A: The formula for Fourier Cosine Transform is given by:…

Q: 5) Answer the following based on the differential equation = y² — y³. a) Find the critical points.…

A: “Since you have posted a question with multiple sub-parts, we will solve the first three sub-parts…

Q: A. Create a distance matrix by using Euclidean distance for the below raw data. (Please write the…

A: Given: A raw data,   X Y A 9 49 B 24 54 C 51 28 D 81 54 E 81 23 F 86 32 To create:…

Q: (d) Lu=ux + Uy + 1

A:

Q: Exercise 2.1.1 Find a general solution to each linear ODE, and then find the specific solution with…

A: Given: The differential equation with the initial conditions is as follows : e u't=ut+2sint ,…

Q: Consider the heat distribution u (x, t) in a semi-infinite rod. Assume that the finite end is kept…

A: Given Data: b To Establish that    u^α,t=100α2π1-e-c2α2tTo show that…

Q: Problem 2: a. Find the differential equation by eliminating the arbitrary constants of the family of…

A: Given: The equation is y=C1tan x+C2sec x. To find: (a)The differential equation by eliminating the…

Q: Create an example that illustrates each type of argument below: a) Deductive: b) Inductive:

A: To create an example that illustrates Deductive and Inductive Argument .

Q: Using the indicial notation, show that: a. (āx b) a = 0 b. c. div(curl v) = 0 curl Vu = 0 for any…

A: To prove: (a) (a¯×b¯)·a¯=0. (b) div (curl v¯)=0. (c) curl (∇u)=0. As per policy, only the first…

Q: Instructions: Determine which of the following “proofs” are correct and which are incorrect. If a…

A:

Q: 5.) Compute the standard factorization of 15!.

A:

Q: Find the differential equation by eliminating the arbitrary constants of the family of curves…

A:

Q: III. Given a homogeneous system of equations = (xn+1 1.2xn-0.3yn Vn+1 = 0.4x + 1.3yn 1. What is the…

A: What is Difference Equation: Any equation with a variable difference in it is a difference equation.…

Q: In the function f(x) = ex cos x the approximate value of f(0.5) using P2 (0.5) is OA. 1.25 OB. 0.5 O…

A:

Q: Let a > 0. Prove that if x is a number such that |x-a| a/2 Let b<0. Prove that if x is a number…

A:

Q: A line passes through A (0,3) and B (3/2,0). Another line, L2, intersects the y axis at (0,2) and is…

A:

Q: The number of non-negative integer solutions to the equation x₁ + x₂ + x3 + x4 + X5 + X6 + x7 = 12…

A:

Q: II. Let f(n) = ryn(1-Yn) and consider the nonlinear difference equation Yn+1 = f(n) or Yn+1 =…

A: What is Difference Equation: Mathematical equivalence that takes into account fluctuations between a…

Q: et ƒj = f(xj), ƒ'; = f'(x;), ƒ!! = f'(x;) and so on, where are equispaced grid points with spacing h…

A:

Q: 2. Suppose that you own real estate whose market value will be V(t) dollars t years from now on.…

A: Suppose we own a real estate property whose market value changes as time passes. Let V(t) be the…

Q: Say whether the following function is injective, surjective, bijective, or none of the above (note:…

A:

Q: Let {n} be a sequence. Let Yn = if {n} is monotonic, 1. Show that n then so is {yn}.

A: What is Monotone Sequence: A sequence can either be constant or monotone. There are two different…

Q: II. Let f(n) = ryn(1-yn) and consider the nonlinear difference equation Yn+1 = f(n) or Yn+1 =…

A: What is Difference Equation: mathematical equality including variations between subsequent values of…

Q: Use the given graph to find the mean, median, and mode of the distribution. *** Find the mean.…

A: Given is a graph.   To Use the given graph to find the mean, median, and mode of the distribution.

Q: 15. (D²+1) y = cos x

A:

Q: Find the differential equation by eliminating the arbitrary constants of the family of curves y = C₁…

A:

Q: Let A, B, C, D, E, and F be the propositions: A: Ann is present B: Bill is present C: Charles will…

A: Given: A, B, C, D, E, and F are the propositions: A:  Ann is present B:  Bill is present C:  Charles…

Q: In Exercises 1-10, determine wheth indicated subset is a subspace of the Euclidean space R". 1. {[r,…

A:

Q: From X = π +0.5 sin (Z), derive it atleast 5 equations where when x = one x is isolated. Stop g(x).

A: We need to derive at least 5 equations of the form: x=g(x) from the equation: x=π+0.5sinx2. Using…

Q: Determine the two-variable function F(x, y) if Fy (x, y) = y sin(xy) + x given that x^2 + πχ2 F(x₁ -…

A:

Q: Let N, H, S, D, R, J, and B be the propositions: N: Mr. Smith is the brakeman's next-door neighbor…

A: Statement: Mr. Smith lives halfway between Detroit and Chicago if and only if Mr. Robinson and Mr.…

Q: Figure 1.5a shows/v+w. Mark the points v+w and v+w and v+w. Restricted by 0 ≤ c≤ 1 and 0 ≤ d ≤ 1,…

A:

Q: . D²y(t) + 12Dy(t) + 36y(t) = 5t³ y(0) = 1; Dy(0) = 0

A:

Q: GIVEN: FIND: 1. AUB 2. ANB 3. CC 4. A\E Let U= {1, 2, 3, ..., 9} A = { 1, 2, 3, 4, 5 } B = {4, 5, 6,…

A:

Q: (b) y' + y2 sint = 0 (c) y'= (cos² t) (cos² 2y) (d) ty' (1-y2)¹/2, t>0

A:

Q: Let N, H, S, D, R, J, and B be the propositions: N: Mr. Smith is the brakeman's next-door neighbor…

A: Since you have asked multiple questions, we will solve the first question for you. If you want any…

Q: Use the REGRESSION feature on a graphing calculator. The total cost of the Democratic and the…

A: