Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
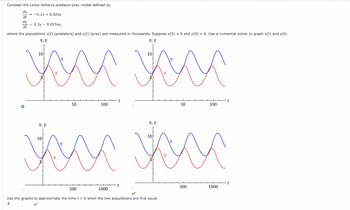
Transcribed Image Text:Consider the Lotka-Volterra predator-prey model defined by
dx
d't
dt
= -0.1x + 0.02xy
= 0.2у - 0.025xy,
where the populations x(t) (predators) and y(t) (prey) are measured thousands. Suppose x(0) = 6 and y(0) = 6. Use a numerical solver to graph x(t) and y(t).
x, y
x, y
10
ким
10
M
50
100
x, y
10
your
м
1000
t
500
Use the graphs to approximate the time t> 0 when the two populations are first equal.
50
x, y
10-
КИМ
и
500
100
1000
t
t
Transcribed Image Text:Use the graphs to approximate the period of each population.
period of x 10
X
period of y
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images
Knowledge Booster
Similar questions
- Consider a crossbow that fires a bolt straight upward from the ground with an initial velocity of 56 m/s. Because of linear air resistance with a drag coefficient p=0.04, its velocity function v=dy/dt satisfies the following initial value problem. dv -=f(tv)= -0.04v-9.8, v(0)=56 dt This problem has an exact solution v(t) = 301e Van-100 Vnin 200 (a) Use a calculator or computer implementation of the Runge-Kutta method to approximate v(t) for 0sts 10 using both n=100 and n=200 subintervals. (Round to four decimal places as needed.) 1 44. 1976 0 25 2 32 8580 -245. Answer parts (a) through (c) below 3 21.9631 H GUCCEED 4 11.4953 5 6 1.4380 -8.2250 ALL 7 17.5091 8 26.4291arrow_forwardLet F(x)= = (a) F(12) Enter the exact answers. (b) F' (12) = X (c) F" (12) = √² + 25 dt. Find the following. 2 i = iarrow_forwardPlease help with letter E (the first picture has the information about the problem needed).arrow_forward
- If s(t) is the position on the x-axis of a particle at time t, then the quantitys(t + h)−s(t) / h represents ?arrow_forwardConsider the discrete-time dynamical system xt+1 = 5xt(1-xt).If xt = 4/5, xt +1 = _____Is x1 = 4/5 an equilibrium for this system? ______Write the updating function rule as f(x) = 5x(1-x).Compute the derivative: f'(x) = ______Evaluate the derivative at the equilibrium: ___________Is the equilibrium stable, unstable or neither? ________arrow_forwardFind g(3), g’(3), and g’’(3)arrow_forward
- Suppose that the amount of phosphorus in a lake at time t, denoted by P(t), follows the equation dP = 3t + 4, with P(0) = 8 dt Find the amount of phosphorus at time t= 14. ..... P(14) =arrow_forwardConsider a theoretical model for mutual inhibition in ecological systems where n > 0 measures the strength of mutual inhibition d dt x(t) = (1/2)" (1/2)" +yn - x d dt (t) = (1/2)" - (1/2)" +x" -y Plot the nullclines and determine the equilibria points for n = 1 and n = 3. Interpret these equilibrium in the ecological setting. Explicitly calculate the local stability of the equilibrium point where x* = y* for gen- eral n. When does the system undergo a qualitative change in behaviour?arrow_forwardSuppose that T =f(t) gives the temperature T (in degrees Fahrenheit) of a pot of coffee t minutes after being brewed. If f '(20) = -3 and f(20) = 125, use a linear approximation (linearization) to estimate the coffee's temperature after 20.4 minutes.arrow_forward
- Suppose the number of bacteria in a culture increases by 50% every hour if left on its own. Assuming that biologists decide to remove approximately one thousand bacteria from the culture every 10 minutes, which of the following equations best models the population P = P(t) of the bacteria culture, where t' is in hours? A. dP = 5P-1000 dt dP B. at dP C. dt dP D. dt E. dP at = 5P-6000 1.5P-6000 = 1.5P-1000 = -5P-1000arrow_forward2. Assume that the population of a colony of Brazilian fire ants, P, is described by the function P(t)= \t+1·e-0.5t is measured in days (t=0 when one begins monitoring the population). (a) Find the initial population, P(0) (include units with your answer). +10t +200. The population here is measured in thousands of individuals, and time, t, %3D %3D (b) Find P (t). (c) Evaluate P (0) (include units with your answer).arrow_forwardthe relationship between aphids, A, ( prey) and ladybugs, L, (preditor) can be described as follows: dA/dt=2A=0.01AL dL/dt=-0.5L+0.0001AL a) find the two critical points of the predator-prey equations b) use the chain rule to write dL.dA in terms of L and A c) suppose that at time t=0, there are 1000 aphids and 200 ladybugs, use the Bluffton university slope field generator to graph the slope for the system and the solution curve. let 0 be less than or equal to A who is less than or equal to 15000 and 0 is less than or equal to L which is less than or equal to 400.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,