
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
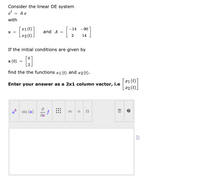
Transcribed Image Text:Consider the linear DE system
a' = A x
with
r1(t)
|x2 (t).
-14 -90
X =
and A =
14
If the initial conditions are given by
x (0) = :
find the the functions #1 (t) and x2 (t).
x1 (t)
[ x2 (t).
Enter your answer as a 2x1 column vector, i.e
ab sin (a)
f
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 8 steps

Knowledge Booster
Similar questions
- Suppose that the position function of a particle moving on a coordinate line is given by s(t) 1³-2t² + 3t -7 in meters, where t is in seconds. (a) Find the velocity and acceleration functions; (b) Analyze the direction of the motion that shows when the particle is stopped, when it is moving forward and/or backward; (c) Analyze the change of speed that shows when it is speeding up and/or slowing down; (d) Find the total distance traveled by the particle from time t =0 to t = 6 seconds.arrow_forwardWhat is the velocity vector?arrow_forward18 > (a) Find the direction for which the directional derivative of the function f (x, y) = 7xy² + 5x² is a maximum at P = (-1,2). (Use symbolic notation and fractions where needed. Give your answer in vector form.) direction: (b) Find the maximum value of the directional derivative. (Use symbolic notation and fractions where needed.) ||Vf(-1,2) || =arrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

