Consider the following two-bond portfolio of option-free bonds; Bond A Bond B Years to maturity 5 years 10 years Coupon rate 5% 5% Par value 1000 1000 Yield to maturity 8% 6% Par amount owned for Bond A: R3,45m For bond B:R2m Market value :Bond A:R30 367.59 (in 000’s) Market value:Bond B:R18 528 (in 000’s) Required: a) Without doing any calculations, which bond would have a higher duration b) Assuming that Bond A is an option-free bond, calculate the bond’s modified duration using Macauly’s Duration. c) Assume that the duration of Bond A and B is 4.2 and 7.5 respectively; determine the duration of the portfolio.
22) Consider the following two-bond portfolio of option-free bonds;
Bond A Bond B
Years to maturity 5 years 10 years
Coupon rate 5% 5%
Par value 1000 1000
Yield to maturity 8% 6%
Par amount owned for Bond A: R3,45m For
Market value
Market value:Bond B:R18 528 (in 000’s)
Required:
a) Without doing any calculations, which bond would have a higher duration
b) Assuming that Bond A is an option-free bond, calculate the bond’s modified duration using Macauly’s Duration.
c) Assume that the duration of Bond A and B is 4.2 and 7.5 respectively; determine the duration of the portfolio.
a)
Bond’s duration measures the interest rate sensitivity to its price. This depends on various factors such the time to maturity of the bonds and its coupon rate. Bonds with higher maturity period are more sensitive to interest rate changes and those with lower coupon rates will take longer time to repay the price of the bond. Hence, when everything is constant a bond with longer maturity will have higher duration. Here, Bond A has a maturity of 5 years whereas Bond B has a maturity of 10 years.
Answer: Therefore, Bond B has higher duration than Bond A.
b)
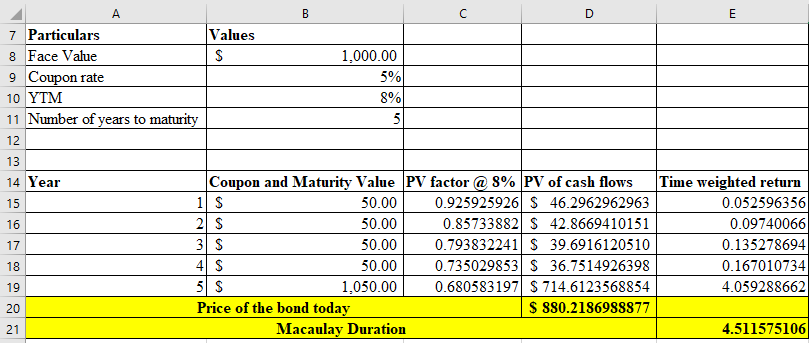
Macaulay’s duration is the weighted average number of days it will take to recover the price of the bond through its coupon and principal payments. It can be calculated in the excel as below:
Excel Workings:
Result:
Modified duration of a bond is calculated simply using the below formula:
Here,
n = number of coupons paid per year = 1
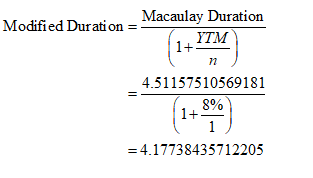
Answer: Therefore, Bond A’s Macaulay duration is 4.51 (rounded to 2 decimal) and Modified duration is 4.18 (rounded to 2 decimal places).
Step by step
Solved in 3 steps with 6 images









