
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
How to use linear independence to prove this
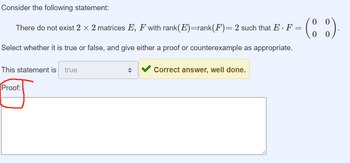
Transcribed Image Text:Consider the following statement:
0
There do not exist 2 × 2 matrices E, F with rank(E)=rank(F) = 2 such that E · F = (88)
Select whether it is true or false, and give either a proof or counterexample as appropriate.
This statement is true
Proof:
Correct answer, well done.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Prove ¬¬A := ¬(¬A) = A ¬(A ^ B) = (¬A) V (¬B) ¬(A V B) = (¬A) ^ (¬B) (Vx € X: E(x)) = (x € X : ¬E(x))arrow_forwardLet f : (0, 1/3 ] → R such that f (x) = x^2.Part 1: Show that f (x) < x.Part 2: Show that f has no fixed point on (0, 1/3 ]. Hint: Assume there were a point c in (0, 1/3 ]such that f (c) = c and derive a contradiction.Part 3: Show that the function f (x) = 1/(1+x^2) from [0, ∞) to [0, ∞) has a fixed point c. Hint: Setf (x) = x and show the resulting equation has a solution in [0, ∞) using the the IVParrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

