Consider the following network, where each number along a link represents the actual distance between the pair of nodes connected by that link. The objective is to find the shortest path from the origin to the destination. (a) For the forward recursion formulation of this problem, how many stages are there, and what arethe states for each stage? (origin) ( 6 f₂(A) = 11 5 B 7 8 6 f₂(C) = 13 f3(D) = 6 6 (Ε f3(E) = 7 (destination) (b) Use forward recursion to solve this problem. However, instead of using the usual tables, show your work graphically. In particular, start with the given network, where the answers already are given for fi (Sn) for four of the nodes; then solve for and fill in f₂ (B) and fi (0). Draw an arrowhead that shows the optimal link to traverse out of each of the latter two nodes. Finally, identify the optimal path by following the arrows from node O onward to node T. (c) Use forward recursion to solve this problem by manually constructing the usual tables for n = 3, n = 2, and n = 1. Some answers are already given, finish the tables by filling in the blank cells.
Consider the following network, where each number along a link represents the actual distance between the pair of nodes connected by that link. The objective is to find the shortest path from the origin to the destination. (a) For the forward recursion formulation of this problem, how many stages are there, and what arethe states for each stage? (origin) ( 6 f₂(A) = 11 5 B 7 8 6 f₂(C) = 13 f3(D) = 6 6 (Ε f3(E) = 7 (destination) (b) Use forward recursion to solve this problem. However, instead of using the usual tables, show your work graphically. In particular, start with the given network, where the answers already are given for fi (Sn) for four of the nodes; then solve for and fill in f₂ (B) and fi (0). Draw an arrowhead that shows the optimal link to traverse out of each of the latter two nodes. Finally, identify the optimal path by following the arrows from node O onward to node T. (c) Use forward recursion to solve this problem by manually constructing the usual tables for n = 3, n = 2, and n = 1. Some answers are already given, finish the tables by filling in the blank cells.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
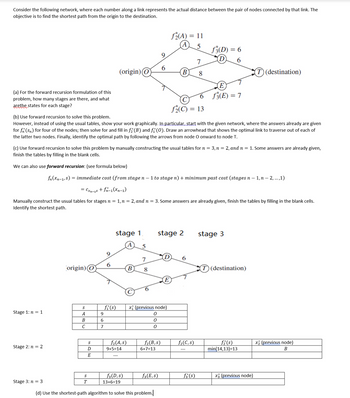
Transcribed Image Text:Consider the following network, where each number along a link represents the actual distance between the pair of nodes connected by that link. The
objective is to find the shortest path from the origin to the destination.
(a) For the forward recursion formulation of this
problem, how many stages are there, and what
arethe states for each stage?
Stage 1: n = 1
Stage 2: n = 2
origin) (
Stage 3: n = 3
S
A
B
C
(b) Use forward recursion to solve this problem.
However, instead of using the usual tables, show your work graphically. In particular, start with the given network, where the answers already are given
for f (Sn) for four of the nodes; then solve for and fill in f2 (B) and fi* (0). Draw an arrowhead that shows the optimal link to traverse out of each of
the latter two nodes. Finally, identify the optimal path by following the arrows from node O onward to node T.
(c) Use forward recursion to solve this problem by manually constructing the usual tables for n = 3, n = 2, and n = 1. Some answers are already given,
finish the tables by filling in the blank cells.
We can also use forward recursion: (see formula below)
S
D
E
S
T
(origin)
fn (xn-1, S) = immediate cost (from stage n - 1 to stage n) + minimum past cost (stages n-1, n-2,...,1)
= Cxn-s + fn-1(Xn−1)
Manually construct the usual tables for stages n = 1, n = 2, and n = 3. Some answers are already given, finish the tables by filling in the blank cells.
Identify the shortest path.
9
6
7
6
stage 1
A
fi (s)
f₂(A, s)
9+5=14
5
7
B 8
f3(D, s)
13+6=19
(d) Use the shortest-path algorithm to solve this problem.
f₂(A) = 11
5
x₁ (previous node)
0
0
0
f₂(B, s)
6+7=13
stage 2
f3(E, s)
6
f₂(C) = 13
7
8
6
f₂(C, s)
ƒ3(D) = 6
6
f3(s)
E
ƒ3(E) = 7
stage 3
(destination)
T (destination)
f₂ (s)
min(14,13)=13
x3 (previous node)
x₂ (previous node)
B
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 5 steps with 49 images
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
