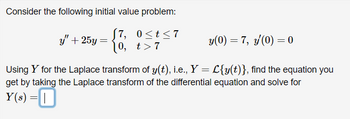
Consider the following initial value problem: 0≤t≤7 t>7 y" + 25y = (7, 10, y(0) = 7, y'(0) = 0 Using Y for the Laplace transform of y(t), i.e., Y = L{y(t)}, find the equation you get by taking the Laplace transform of the differential equation and solve for Y(s) =|

Q: 3 The reduced row echelon form of the matrix A = 0 0 Find a basis for the null space of A and the…

A: The reduced row echelon form of the matrix  is .We have to find the basis for the null space of A…

Q: 6. Find all solutions of the equations: (i) 2 sinx-1=0 (ii) cos²x-3 cos x + 2 = 0 7. Convert the…

A: As Per Bartleby  Answering Guidelines We Solve Only First One Problem

Q: If 6(8+34)/s (s^2+10s+34) =A/s+B/(s+5-13)+C/(s+5+13}, C. O

A: We have We have to find the value of

Q: Describe all solutions of Ax = 0 in parametric vector form, where A is row equivalent to the given…

A:

Q: Determine the amplitude, period, and displacement for the function y 4 The amplitude of the function…

A: The given function is .We have to find the amplitude, period, displacement of the function and…

Q: I keep getting the wrong answer can you help me

A: Use hyperbolic functions to parametrize the intersection of the surfaces  and (Use symbolic notation…

Q: Consider the following graph on the interval -150° < x < 225°: 150 -120 -90 60 30 -4- 3- 2 H + 2-…

A: 1. Here given function has neither maximum value nor minimum value .Hence there is no amplitude of…

Q: 1) Suppose that A² = A and B is a diagonal matrix similar to A. Prove that B2 = B and that the…

A:

Q: Find the roots of the equation 2 x³ - 16x² + 42x - 36 = 0 given that it has a root of multiplicity…

A:

Q: Simplify the following expression: 9.com Re (-jet)

A:

Q: Consider the function f(x) = X n 1+nx - if n < x < n + 1 for n even if n < x <n+ 1 for n odd (a)…

A:

Q: Question 3: Simplify the following expression: Re(-jes)

A:

Q: ***********... In how many ways can four people boarding a bus be seated if the bus has nine vacant…

A: According to the question, The problem is a permutation problem. In mathematics, a permutation of a…

Q: Let W be the subspace of P3 where Find a basis for W. W = {p(x) = P3 with p'(4) = p'(-2), p(-3) = 0,…

A: is a subspace of  where

Q: Consider the following matrix ^-18 11]. A = (a) Find the eigenvalues and the eigenvectors of this…

A:

Q: The graph of f(t) is given below: 1.0 (Click on graph to enlarge) a. Represent f(t) using a…

A:

Q: determine convergent or divergent and why

A: We know that…

Q: (Optional) Torsion of a curve is defined as T = [r′(t) × r' (t)] · r'' (t) ||r' (t) x r"(t)||² is a…

A:

Q: The time to complete an exam is approximately Normal with a mean = 53 minutes and a standard…

A: =53 and =3

Q: Problem 1 Give an example of a power series that converges precisely on 1 < x < 5.

A:

Q: Use hyperbolic functions to parametrize the intersection of the surfaces x² - y2 = 25 and z = 5xy.…

A: Surfaces : ,

Q: 20. HHO -4 7 5 -6 8 9

A:

Q: suppose that A is an nxn matrix It A² = A then A must be the identity. Cuote assume that no1).

A: is an  matrix.Also, .

Q: Find the expression of Px² qx (x + t), P¸μ(x+t) with steps, if s(x + t) = s(x)(1-t) s(x + 1)t…

A:

Q: 10. Let F be the vector field F(x, y, z) = r/|r|5, where r = xi+yj + zk. If S is the sphere x² + y²…

A: According to guidelines we can do only first question thank youWe use divergence theorem to find…

Q: 1 8 Find a basis for the subspace of R³ consisting of all vectors 2 such that 6x1 - 7x2 - 4x3 = 0. 3…

A:

Q: X У 4 7 5 10 6 8 7 14 9 17

A: Least square regression line where  and Givenx45679y71081417

Q: 8. Sketch the graph of the combined function of y = (g - f)(x) for the following functions of f(x)…

A: From given fig.we can write g(x) = 1- |x|      and    f(x) = x^2-4 .

Q: find the equation of the tangent plane and normal line to the surface x^2+y^2-2xy-x+3y-z^2 at point…

A:

Q: 10 (d) enclosed between the curves y = 1+² and y = 4-x,

A: We have to calculate the area enclosed by the curve  and

Q: 3. y' = y³, y(0) = 1

A: As you mentioned Q-3 with three parts as per norm.GivenHere and The Euler's method iteration

Q: Determine whether the series converges; if so, find its sum. If the series diverges, indicate that…

A: We have to determine whether the series converges or diverges of the following series:If it…

Q: Write the matlab code for the above pathline and streaklines graph

A: As per the question we are given pathline and streakline plots and we have to recreate those plots…

Q: Let W be the subspace spanned by Find a basis for W and the dimension of W. -3 (Note that the…

A:

Q: (b). Find a general solution to the given Cauchy-Euler equation for t > 0. t²y" - 3ty' + 3y =…

A: To Find: A general solution to the given Cauchy-Euler equation for…

Q: 2. Write a program in MATLAB to numerically solve for the concentration distribution in a duct of…

A: note :Since you have posted multiple questions, we will provide the solution only to the question…

Q: In Exercises 3-6, the vector X is in a subspace H with a basis B = {b₁,b₂}. Find the B-coordinate…

A:

Q: Solve of the Boundary-Value Problem (BVP) by the method of seperation of variab u, (0, 1) = 0, u(2.…

A:

Q: Werify that (x)=- 1-ce* dy Substitute (x) for y and find the derivative to substitute for dx…

A: We have to verify that  where c is an arbitrary constant is a one parameter family of solution to

Q: wrong answer. can you do it again

A:

Q: Find the largest and smallest values (absolute maximum and minimum) of In(4x+1 h(x) on the interval…

A: To Find:Absolute maximum and minimum in

Q: m Determine for which values of m the function p(x)=x™ is a solution to the given equation. 2d²y dx²…

A:

Q: The McDonnell Douglas (now Boeing) F-15E Strike Eagle is an American all-weather multirole strike…

A:

Q: M (x₁+x2) dV2(x), where M is the 2-manifold in R4 given parametrically as shown. x = (U₁+U₂,4₁…

A: The solution is given by

Q: Recall that the Fibonacci numbers are defined by Fo= 0, F₁ = 1, Fn-1 + Fn-2 for n ≥ 2. Show that lim…

A: The Fibonacci numbers are defined by   ------(1)                                    Assume that…

Q: The graph of f(t) is given in the figure. Represent f(t) using a combination of Heaviside step…

A:

Q: - Evaluate, and express your answer as a fraction or -2 integer: 64 1 8

A: Solution:Given expression: we have to evaluate the given expression

Q: Problem 2 Solve the initial value problem. Solution: (1+z)y' + y = cos(z) y(0) = 1

A: (1+x)y'+y=cosx, y(0)=1

Q: Problem 5 Find the domain and range of the following functions. 1. The function that assigns to each…

A: 1.Given:The function that assigns to each pair of positive integers the first integer of the…

Q: Express the solution of the given ini value problem as a sum of two oscillations, as in Eq. (8).…

A: The general solutio of linear differential equation is the sum of complementary solution and…