
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
![**Problem Statement:**
Consider the equation below.
\[ r = \frac{5}{2 + 3\sin(\theta)} \]
**Tasks:**
(a) **Find the eccentricity.**
\[ e = \]
(b) **Identify the conic.**
- Ellipse
- Parabola
- Hyperbola
- None of the above
(c) **Give an equation of the directrix (in Cartesian coordinates).**
\[ \text{Equation:} \]
(d) **Sketch the conic.**
**Graph Analysis:**
1. **Top Left Graph:**
- This graph appears to show a parabola opening upwards. The vertex is at the origin (0,0), and the parabola is symmetrical across the y-axis. The directrix is shown as a horizontal dashed line below the vertex.
2. **Top Right Graph:**
- This graph illustrates a parabola opening to the right. The vertex is at the origin, and the parabola is symmetrical across the x-axis. The directrix is represented as a vertical dashed line to the left of the vertex.
3. **Bottom Left Graph:**
- This is a graph of a hyperbola with branches opening left and right. The asymptotes are shown as dashed diagonal lines intersecting at the origin.
4. **Bottom Right Graph:**
- The graph shows a hyperbola with vertical and horizontal branches. The asymptotes are diagonal dashed lines that cross at the origin, indicating the center of the hyperbola.
Select the correct graph according to the conic section determined from the given equation.](https://content.bartleby.com/qna-images/question/f95d43da-01ae-4bee-8168-060148562ed2/1e6b0e88-c543-4454-be9d-54dd8758e353/x1pt7g_thumbnail.png)
Transcribed Image Text:**Problem Statement:**
Consider the equation below.
\[ r = \frac{5}{2 + 3\sin(\theta)} \]
**Tasks:**
(a) **Find the eccentricity.**
\[ e = \]
(b) **Identify the conic.**
- Ellipse
- Parabola
- Hyperbola
- None of the above
(c) **Give an equation of the directrix (in Cartesian coordinates).**
\[ \text{Equation:} \]
(d) **Sketch the conic.**
**Graph Analysis:**
1. **Top Left Graph:**
- This graph appears to show a parabola opening upwards. The vertex is at the origin (0,0), and the parabola is symmetrical across the y-axis. The directrix is shown as a horizontal dashed line below the vertex.
2. **Top Right Graph:**
- This graph illustrates a parabola opening to the right. The vertex is at the origin, and the parabola is symmetrical across the x-axis. The directrix is represented as a vertical dashed line to the left of the vertex.
3. **Bottom Left Graph:**
- This is a graph of a hyperbola with branches opening left and right. The asymptotes are shown as dashed diagonal lines intersecting at the origin.
4. **Bottom Right Graph:**
- The graph shows a hyperbola with vertical and horizontal branches. The asymptotes are diagonal dashed lines that cross at the origin, indicating the center of the hyperbola.
Select the correct graph according to the conic section determined from the given equation.
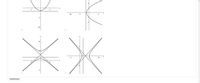
Transcribed Image Text:The image contains four graphs arranged in a 2x2 grid, each representing different conic sections with their respective axes labeled.
**Top Left Graph:**
- This is a parabola opening upwards.
- Its vertex is at the origin (0,0) on the coordinate plane.
- The x-axis and y-axis are marked with values ranging approximately from -10 to 10.
**Top Right Graph:**
- This graph displays a hyperbola opening horizontally.
- The center of the hyperbola is at the origin.
- The x-coordinate values range from approximately -10 to 10, and the y-coordinate values range from -5 to 5.
**Bottom Left Graph:**
- This is a hyperbola with its transverse axis in the vertical direction.
- The graph shows two branches opening upwards and downwards.
- The axes are labeled with x ranging from approximately -10 to 10 and y from -10 to 10.
**Bottom Right Graph:**
- Another hyperbola graph, with branches opening to the right and left.
- The center is near the origin with asymptotes approaching diagonal lines.
- The axes range between x: -10 to 10, y: -10 to 10.
Below these graphs, there are selectable radio buttons which likely serve as multiple-choice options for understanding or identifying the conic sections. At the bottom of the image, a "Submit Answer" button is visible, indicating an interactive element likely for assessment purposes.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

