
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
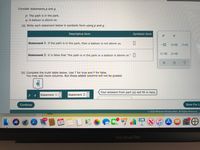
Transcribed Image Text:Consider statements p and q.
p: The path is in the park.
q: A balloon is above us.
(a) Write each statement below in symbolic form using p and q.
Descriptive form
Symbolic form
q
Statement 1: If the path is in the park, then a balloon is not above us.
OvO
O-0
Statement 2: It is false that "the path is in the park or a balloon is above us." I
(b) Complete the truth table below. Use T for true and F for false.
You may add more columns. But those added columns will not be graded.
Your answers from part (a) will fill in here.
Statement 1:
Statement 2:||
Continue
Save For L
© 2020 McGraw-Hill Education. All Rights Reserved.
30
MacBook Pro
Transcribed Image Text:F
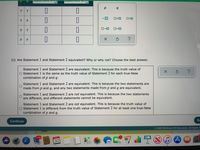
(c) Are Statement 1 and Statement 2 equivalent? Why or why not? Choose the best answer.
Statement 1 and Statement 2 are equivalent. This is because the truth value of
O Statement 1 is the same as the truth value of Statement 2 for each true-false
combination of p and q.
Statement 1 and Statement 2 are equivalent. This is because the two statements are
made from p and q, and any two statements made from p and q are equivalent.
Statement 1 and Statement 2 are not equivalent. This is because the two statements
are different, and different statements cannot be equivalent.
Statement 1 and Statement 2 are not equivalent. This is because the truth value of
O Statement 1 is different from the truth value of Statement 2 for at least one true-false
combination of p and q.
Sa
Continue
© 2020 McGraw-Hill Education. All Rights F
,762
30
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Write the following compound statement in symbolic form and construct a truth table. the soda is in the cooler and the oranges have been peeled p: the soda is in the cooler. q: the oranges have been peeledarrow_forwardWhich conclusion follows from the 2 given statements ?arrow_forwardConstruct a truth tablearrow_forward
- Write the statement in symbolic form. Then construct a truth table for the symbolic statement. You'll love the new horror movie if and only you're afraid of haunted houses, or you won't find it very entertaining.arrow_forwardUse a truth table to determine whether the statements are equivalent. She is unemployed or she does not have a high school diploma. If she is unemployed, then she does not have a high school diploma.arrow_forwardLet p, q, and r represent the following simple statements. p: I eat bananas. q: I like ice cream. r I like to eat. Write the following compound statement in its symbolic form. If I do not eat bananas then: I do not like ice cream and I do not like to eat. The symbolic form isarrow_forward
- Translate the compound statement into symbolic form and then construct the truth table for the expression. (That is, complete the truth table; the title row and columns.) He is a not mathematician and he is not a musician. P qarrow_forwardLet p = Sam owns a sedan. q = Joan owns an SUV. Translate the following statement into symbols. Then determine under what conditions the compound statement is true. Note: A truth table may be needed. Sam does not own a sedan, but Joan does not own a SUV.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

