
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
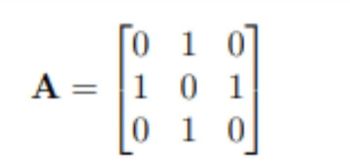
Transcribed Image Text:0 1 0
A = 1 0
010

Transcribed Image Text:Consider an Nx N matrix A with N orthonormal eigenvectors x such that Ax' = ₁x¹,
where the X, is the eigenvalue corresponding to eigenvector x'. It can be shown that such
a matrix A has an expansion of the form:
A = ΣA₁x¹)(x¹=A₁x²(x¹).
i) Show that if the eigenvalues are real then A, as defined through the above expansion,
is Hermitian.
ii) Using the result for A show that the Nx N identity matrix can be written as
N
I= Σx'(x¹)¹.
iii) In proving this result for the identity matrix you have used the fact that the vectors
{x} are eigenvectors of a matrix A. Is this essential or is there a milder requirement
possible? If so, what is it? Justify your answers.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 5 steps with 6 images

Knowledge Booster
Similar questions
- The matrix A = has eigenvalues λ = 1, 2, 3, 4. Is - B -4 5 5 5 -6 26 6 -7 0 3 7 -8 5 5 9 = -3 55 5 -6 3 6 6 -7 0 4 7 -8 5 5 10 diagonalizable? Without calculating eigenvectors or eigenvalues, explain why or why not (you will lose points if you calculate eigenvectors or eigenvalues).arrow_forwardSuppose v is an eigenvector of a matrix A with corresponding eigenvalue A, and suppose c is a (fixed) scalar. Show based on the definition of eigenvector and eigenvalue that v is an eigenvector of cI – A with corresponding eigenvalue c – A.arrow_forward
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

