Question
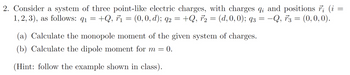
Transcribed Image Text:2. Consider a system of three point-like electric charges, with charges q; and positions ; (i =
1,2,3), as follows: q₁ = +Q, F₁ = (0, 0, d); 92 = +Q, F₂ = (d, 0, 0); 93 = -Q, 73 = (0,0,0).
91
q2
(a) Calculate the monopole moment of the given system of charges.
(b) Calculate the dipole moment for m = 0.
(Hint: follow the example shown in class).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Similar questions
- For problem 4 part b in square centimeters using inner and outer radii of the spherical capacitor of a = 5.49 cm and b = 1.05 a, respectively. (Answer In 5 sig. figs.)arrow_forwardA line charge of infinite length lies along the z axis and carries a uniform linear charge density of pe C/m. A perfectly conducting cylindrical shell, whose axis is the z axis, surrounds the line charge. The cylinder (of radius b), is at ground potential. Under these conditions, the potential function inside the cylinder (p b. (d) Find the stored energy in the electric field per unit length in the z direction within the volume defined by p> a, where a < b.arrow_forwardThe following sequence of problems guides you through the calculation of the total electrie field at a target point in space when there are two source partieles. We'll stick to two dimensions (get rid of the z-axis) just to reduce some of the arithmetic. The source partieles are both located on the z-axis with source 1 at z = 5 em and source 2 at zz = -5 cm. Source 1 has charge -5 uC while source 2's charge is 3 µC. 2. First, calculate the electric field vector due to source I at the target location, (5,6) em. [Enter your answer with the following format: X*i+Y*j. where you substitute the numerical values of the components along the z and y directions in place of the "X and "Y' in the expression. The letters i and j represent the unit vectors along different directions. Use the asterisks to denote multiplication. Make sure to convert your units to standard MKS base units and use two-decimal precision. Denote powers of ten with engineering notation, for example 1.23 x 10 should be…arrow_forward
- Consider a rod of length L carrying a charge of q distributed uniformly over its length. Where applicable, let V(r→∞)=0. a) What is the voltage V at point P (at distance a away from the near end of the rod) due to the charge over the length of the rod? Express your answer in terms of given parameters (L,q,a) and physical constants b) Calculate the electric field at point P by differentiating V with respect to a. Let positive sign of E indicate direction of electric field pointing away from the rod.arrow_forwardProblem 1. Prove that for a vacuum-dielectric interface at glancing incidence ri→-1 (see Fig. 4.49 from textbook, also on slide 7 in Lecture 4). In the same figure, if a is the angle that the curve r(0.) makes with the vertical at 0; = 90°, then: Vn2 – 1 tana, 2 1.0 0.5 Op -0.5 56.3° -1.0 30 60 90 0; (degrees) Figure 4.49 The amplitude coefficients of reflection and transmission as a function of incident angle. These correspond to external reflection n; > n; at an air-glass interface (n = 1.5). Amplitude coefficients ofarrow_forwardDetermine E at (2, 0, 2)m due to three standard charge distributions as follows: a uniform sheet at x = 0 m with ρs1=(13π)nCm2ρs1=(13π)nCm2, a uniform sheet at x = 4 m with ρs2=(−13π)nCm2,ρs2=(−13π)nCm2, and a uniform line at x = 6 m, y = 0 m with ρl=−2nCmρl=−2nCm.arrow_forward
- Problem 3.36 (3rd edition): Two long straight wires, carrying opposite uniform line charges +1, are situated on either side of a long conducting cylinder (Fig. 3.39). The cylinder (which carries no net charge) has radius R, and the wires are a distance "a" from the axis. Find the potential at point 7. (Hint: you can use solution of problem 2.47) R a aarrow_forwardAn insulating solid sphere of radius 3 m has 15 C of charge uniformly distributed throughout its volume. Calculate the charge contained in a Gaussian surface having a radius 1/2 that of the sphere. Present your answer accurately to 2 decimal numbers i.e 3.20. Do not include units!arrow_forwardA particle of charge e and mass m is located at the midpoint of the line joining two fixed collinear dipoles with unit charges as shown in the figure. (The particle is constrained to move only along the line joining the dipoles). Assuming that the length of the dipoles is much shorter than their separation, the natural frequency of oscillation of the particle is iiarrow_forwardAn uncharged, infinitely long conducting cylinder of radius a is placed in an initially uniform clectric ficld E = Eoi, such that the cylinder's axis lics along the z axis. The resulting clectrostatic potential is V (x, y, z) = Vo for points inside the cylinder, and Ega?x x² + y? V (r, y, z) = Vo – Egx + for points outside the cylinder, where Vo is the (constant) clectrostatic potential on the conductor. Usc this expression to determine the resulting clectric ficld, E.arrow_forward12. 2.10 Four masses 10 g each are tied together by 10 cm strings to make a square as shown. Two of the masses carry a charge of 2 μC. The string between the two charged masses is cut and the system begins to move. What is the maximum speed of the masses in m/s? Do not consider gravity or friction. You can imagine the masses to be on a horizontal frictionless table. Enter answer here Windowarrow_forwardA sphere of radius R carries a polarization that follows P(7) = ke¯" f, where k is a constant wit the appropriate unit, and 7 is the vector from the center of the sphere. a) Calculate the surface bound charge density o,(7). b) Calculate the volume bound charge density pp(7). (Be careful about the spherica coordinates!) c) Find the potential V(7) inside and outside of the sphere. d) Find the electric field E(7) inside and outside of the sphere.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios