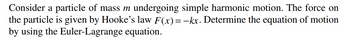
Consider a particle of mass m undergoing simple harmonic motion. The force on the particle is given by Hooke's law F(x)=-kx. Determine the equation of motion by using the Euler-Lagrange equation.

An electron undergoes simple harmonic motion with the acceleration shown below: ax(t)=−amaxsin(2t/T)  with amax=5839 ms2  and T=316 seconds. Assuming that the only motion is oscillatory (ignoring overall translation), what is the maximum speed of the electron? What is the amplitude of the electron's position?

Quartic oscillations Consider a point particle of mass m (e.g., marble whose radius is insignificant com- pared to any other length in the system) located at the equilibrium points of a curve whose shape is described by the quartic function: x4 y(x) = A ¹ Bx² + B² B²), (1) Where x represents the distance along the horizontal axis and y the height in the vertical direction. The direction of Earth's constant gravitational field in this system of coordinates is g = −gŷ, with ŷ a unit vector along the y direction. This is just a precise way to say with math that gravity points downwards and greater values of y point upwards. A, B > 0. (a) Find the local extrema of y(x). Which ones are minima and which ones are maxima? (b) Sketch the function y(x). (c) What are the units of A and B? Provide the answer either in terms of L(ength) or in SI units. (d) If we put the point particle at any of the stationary points found in (a) and we displace it by a small quantity³. Which stationary locations…

Consider the schematic of the single pendulum. M The kinetic energy T and potential energy V may be written as: T = ²m²²8² V = -gml cos (0) аас dt 80 The Lagrangian L is given by L=T-V, and the Euler-Lagrange equations for the motion of the pendulum are given by the following second order differential equation in : ас 80 = 11 = 0 Write down the second order ODE using the specific T and V defined above. Please write this ODE in the form = f(0,0). Notice that this ODE is not linear! Now you may assume that l = m = g = 1 for the remainder of the problem. You may still suspend variables to get a system of two first order (nonlinear) ODEs by writing the ODE as: w = f(0,w) What are the fixed points of this system where all derivatives are zero? Write down the linearized equations in a neighborhood of each fixed point and determine the linear stability. You may formally linearize the nonlinear ODE or you may use a small angle approximation for sin(0); the two approaches are equivalent.

The data given would be the following: 1(t) = -9.8 m/s2 and p(1)= 10 k and d(1) = 19.8 m/s. Using this, determine the position function p(t) using antiderivatives and the initial value data

Calculate the energy, corrected to first order, of a harmonic oscillator with potential:

A particle of mass m described by one generalized coordinate q movesunder the influence of a potential V(q) and a damping force −2mγq˙  proportional to its velocity. Show that the following Lagrangian gives the desired equation of motion: L = e2γt(1/2 * mq˙2 − V (q))