
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Consider a matrix A with N orthonormal eigenvectors {xi} and eigenvalues {λi}. Construct the matrix S from the eigenvectors of A as S = [x1 x2 · · · xN], where each column of S is an eigenvector of A. Because S is constructed from a set of linearly independent
Now consider the action of An on a general vector y in this N dimensional space. We wish to evaluate Any. It is proposed that we start by expanding y as provided (image).
Explain why y can be expanded as shown (quote relevant theorems/results). Find an expression for the coefficients ai in terms of a suitable inner product.
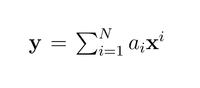
Transcribed Image Text:N'
y = E, a;x'
i=D1
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 43 images

Knowledge Booster
Similar questions
- Let A be a symmetric n x n matrix. Let A1 and A2 be two eigenvalues with eigenvectors vị and v2 for A, respectively. Show that vi and v2 are orthogonal.arrow_forwardLet M be a 2 × 2 matrix with eigenvalues ₁ = -1.2, A2 = 1 with corresponding eigenvectors Consider the difference equation with initial condition Xo = 5 3 V₁ = V2 = 2 xk+1 = Mxk Write the initial condition as a linear combination of the eigenvectors of M. That is, write x0 = c1V1 + C₂ V₂ = In general, xk= V1+ V2 ) * vi+ k ) v2 Specifically, x4 = For large k, xk≈ karrow_forwardLet A be a nxn symmetric matrix with real entries. (a) Show that if A is an eigenvector for A, then X must be a real number. (b) If A1 and A2 are two eigenvalues for A with vị and v2 eigenvectors, respectively. Then vi and a2 are orthogonal.arrow_forward
- the matrix A= }] has eigenvalues A₁ = 1 and A₂ = 5. The bases of the eigenspaces are v₁ = -12 Find an invertible matrix S and a diagonal matrix D such that S-¹AS = D. S= D= and v₂ = , respectivelyarrow_forwardLet A be a arbitrary n x n matrix, Show that if A1 and A2 are two eigenvalues with A1 # ^2 and eigenvectors vi and v2, respectively. Show that vị and v2 are linerly independent.arrow_forwardProve that the sum of two negative definite matrices A and B is negative definite (A+B) meaning that for matrix (A+B) all eigen values will be negative or have negative real partsarrow_forward
- I got some wrong but don't know which ones or why. Thank you.arrow_forwardLet x = Express as a linear combination of 71, 72, and 73, and find Az. Az = -0--0-0 -1,72 = 3 be eigenvectors of the matrix A which correspond to the eigenvalues ₁-3, A₂ = -2, and A3 = 0, respectively, and let v₁+ V1 = √2+ ~2000 7 x = -5 -8 V3. = 4 2arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

