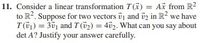
11. Consider a linear transformation T(K) = Ax from R?to R?. Suppose for two vectors vj and üz in R? we haveT(01) = 301 and T (52) = 402. What can you say aboutdet A? Justify your answer carefully.

Answered: Image /qna-images/answer/6a0b4f95-871c-4378-8f39-d75706b6efc1.jpg

Answered: Consider a linear transformation T() =…

Consider a linear transformation T() = Ax from R2 to R. Suppose for two vectors ūj and vz in R? we have T(1) = 301 and T(02) = 402. What can you say about det A? Justify your answer carefully.

Advanced Engineering Mathematics

10th Edition

ISBN:9780470458365

Author:Erwin Kreyszig

Publisher:Erwin Kreyszig

Chapter2: Second-order Linear Odes

Section: Chapter Questions

Problem 1RQ

See similar textbooks

Similar questions

Let e1, e2, èz be the standard unit vectors along the coordinate axes in R³. Let S and T be the linear transformations defind in R³. Show that if S(टे) = T(टे), S( हे ) %3D T(टे.), S(टेs) = T(ेs) then S(7) = T(7) for any 7 e R³.
Find the coordinate vector [x]; of x relative to the given basis B= (b1,b2}. 13 -3 X = - 5 b1 b2 -2 - 1 [x]s
1. Let T : R² → R³ be a linear transformation such that T(e1) = u1 and T(e2) = u2, where e1, e2 8 is the standard unit vectors of R² and u1 3 and u2 = 2. Then find T 1 -2 6.
Suppose T: R2 R3 is a linear transformation. Let u, v and w be the vectors given below, and suppose that T(u) and T(v) are as given. Find T(w). 18 22 T(u) = 20 25 -7 -8 u= 5 2 V = 0 T(w) = 0 0 5 3 W = -20 10 T(v) =
Suppose T: R¬R2 is a linear transformation. Let u and v be the vectors given below, and suppose that T(u) and T(v) are as given. Find T(-u-3v). 14 22 v = 4 T(u) = T(v) = 13 es u = 2 21 es T(-u-3v) = 0 %3D es 3.
Consider the vectors i and i shown below, which are related by a reflection through the x-axis. y Suppose T: R' → R? is a linear transformation such that T(e1) = ei and T(7) = 2e1. Find T(w) or explain why it cannot be determined. Warning: The picture does not indicate any scale on the y-axis. That means we cannot estimate the y-components of these vectors j and w (aside from the fact that their y-components are clearly not zero)! 12
Suppose T: R³-R² is a linear transformation. Let U, V and W be the vectors given below, and suppose that T(U) and T(V) are as given. Find T(W). -3 3 2 3 ਪ = -3 -1 0 T(W) = 0 0 V = -3 W = | 3 - 1 T(I) = 0 T(V) = 0 -3
Suppose T: R³→R² is a linear transformation. Let U and V be the vectors given below, and suppose that T(U) and T(V) are as given. Find T(−U+2V). 2 U = 1 3 4 V = 3 4 0 T(-U+2V) = 0 0 -6 [:] 6 T(U)= -9 [3] 9 T(V) =
If T:R²→R³ is a linear transformation and the action of T on the special vectors U and V is as given, find a formula for T(X), where X is any vector in R². -10 [13] 10 4 -3 -4 u ¹] V-3] = = -2 -3 T X [1] = 0 T(U)= 7 T(V) =
Suppose T: R² R³ is a linear transformation. Let u, v and w be the vectors given below, and suppose that T(u) and T(v) are as given. Find T(w). 21 T(v) = 18 31 u= 2 V = T(w) = 0 0 2 5 W = 5 12 9 T(u) = 7 13
Let e1, e2, e3 be the standard unit vectors along the coordinate axes in R³. Let S and T be the linear transformations defind in R³. Show that if S(2) = T(7), s(2) = T(72), s(23) = T(73) then S(7) = T(7) for any 7 E R³.