
Consider a hypothetical consumer named Hayden who is shopping for bread and brie. The graph with bread and brie on the axes presents the utility‑maximizing combinations of bread and brie that Hayden chooses when the
The two points and associated values in the graph for bread and brie combinations correspond to points A and B in the graph of the demand curve for brie. What are the specific prices and quantities of brie associated with points A and B on Hayden's demand curve?
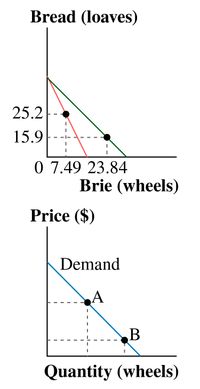
The graph shows two points and associated values for bread and brie combinations correspond to points A and B in the graph of the demand curve for brie where
The price for the brie is $4 and $6per wheel.
The price for the bread is $1 per loaf
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps

- Consider the figures to the right. Suppose that the individual currently consumes 5 digital apps. What happens to the person's total utility if they reduce their consumption to 4 units? Why does this fact imply that the marginal utility curve cuts through the horizontal axis of the lower figure between the fourth and fifth app consumed? Reducing consumption to 4 apps from 5 apps leaves total utility at utils in the upper , which is the figure. Hence, the marginal utility between these two quantities of apps equals value of the axis in the lower figure. Thus, the marginal utility curve crosses the axis of the lower figure between units 4 and 5. (Enter your responses as whole numbers.) Marginal Utility (utils per week) 6- 4- 22 Total Utility (utils + q r per week) 14- 12- 10- 20 ø Ø 18- 04 0 Downloaded Digital Apps Utilized per Week Downloaded Digital Apps Utilized per Week G Qarrow_forwardjust question 1arrow_forwardPlease see below. I need help with this.arrow_forward
- Another instance when people are likely not to spend a dime (or a minute) on an item is when they have a dislike for mixing the item with other items available. In this case, we say the consumer has ‘non-convex preferences’ and indifference curves are bowed out from the origin. In plain language, the consumer has a preference for binging. We often feel this way towards our favorite social media app. Consider a kid who has four hours a day to spend on social media. They enjoy spending time on Snapchat (x) or spending time on Twitter (y). a) Write the kid’s time constraint and illustrate it in a graph where you measure time spent on Snapchat along the horizontal axis and time spent on Twitter along the vertical axis. This kid’s utility from time spent on Snapchat and time spent on Twitter is U(x,y) = 4x2+ y2. b) In your graph, draw a couple of the kid’s indifference curves. Notice how the kid’s |MRSY,X| increases along each curve as he spends more time on Snapchat and less time on…arrow_forwardplease helparrow_forwardSuppose that U(f,c) = f + 8c^(1/2)is a utility function that describes Amelia’s preferences over two goods: fish(f)and custard (c). For the following, think of fish as the good graphed on the horizontal axis.a. Derive an expression for her marginal utility (Uf)from a small increase in f holding c fixed. Also find themarginal utility for custard (Uc).b. What is Amelia’s marginal rate of substitution (MRS)? Give a brief (2 sentences maximum) intuitivedescription of what MRS represents. If Amelia has 4 units of custard, holding her utility constant, howmany units of custard would she be willing to give up in order to get one more unit of fish?c. Graph Amelia’s indifference curve for a utility level of 40. Be sure to specify at least 3 bundles of goodson the indifference curve.d. Does the fact that Amelia’s indifference curve intersects with the custard axis violate any of the 5properties of indifference curves? Briefly support your answer.e. Give another utility function that represents…arrow_forward
- Huang is determining how much Coke and Pepsi he will buy. Use the information in italics to answer the bolded question below. • Huang's preferences for Coke (C) and Pepsi (P) are represented by the following utility function: U = 2C + 3P • Huang has $12 to spend on soft drinks. • The price of Coke (P) is $0.50/can. • The price of Pepsi (Pp) is $1.00/can. Which of the following statements referring to Huang's preferences is incorrect. O Huang does NOT experience diminishing MRS. If Huang gives up two cans of Pepsi, he needs to purchase 3 cans of Coke to remain equally satisfied. Pepsi and Coke are perfect substitutes for Huang O None of the above statements are incorrect.arrow_forwardJackie has a budget of $36 per month to spend on snacks. She can spend this budget on bags of potato chips (C) and Hershey chocolate bars (H). Potato chips cost $4 per bag, while Hershey bars cost $1 per bar. The utility that Jackie receives from consuming potato chips and Hershey bars is represented by the following utility function: U=3C2 H. Given that Jackie seeks to maximize her utility, find the number of potato chip bags and Hershey chocolate bars that Jackie will purchase each month.arrow_forwardSmith and Jones are stranded on a desert island. Each has in her possession some slices of ham (H) and cheese (C). Smith prefers to consume ham and cheese in the fixed proportion of 2 slices of cheese to each slice of ham. Her utility function is given by Us = min(10H, 5C). Jones, on the other hand, regards ham and cheese as substitutes – she is always willing to trade 3 slices of ham for 4 slices of cheese, and her utility function is given by UJ = 4H + 3C. Total endowments are 100 slices of ham and 200 slices of cheese. a. Draw the Edgeworth Box diagram for all possible exchanges in this situation. What is the contract curve for this exchange economy? b. Suppose Smith’s initial endowment is 40 slices of ham and 80 slices of cheese (Jones has the remaining ham and cheese as her initial endowment). What mutually beneficial trades are possible in this economy and what utility levels will Smith and Jones enjoy from such trades? c. Now imagine a new endowment in which Smith has 60 slices…arrow_forward
- Lucas likes lemon soda (X) and chips (Y). His utility function is given by: U (X, Y) = X0.2Y0.8 He earns $40 per week to spend on lemon soda (X) and chips (Y). The prices of lemon soda and chips are $2 and $4 respectively. Find out Lucas’s utility-maximizing bundle of lemon soda and chips (X*, Y*). Set up the utility-maximization problem and find out the price ratio of these two goods. Find out Lucas’s marginal utility of lemon soda (MUX) and marginal utility of chips (MUY). Calculate the MRSXY . Set up the optimal tangency condition and solve for Y in terms of X. Solve for Lucas’s optimal consumption bundle of lemon soda (X*) and chips (Y*). Draw the optimal consumption bundle on the budget constraint BC1 in Q1. Denote it as Bundle A. Make sure to indicate the optimal consumption of lemon soda (X*) and chips (Y*). Draw an indifference curve that is tangent to the budget constraint at Bundle A. Calculate the value of the MRSXY (the value not the formula) at the optimal…arrow_forwardFang likes playing badminton with her friends. Her utility function for playing badminton every week is given by U(t) = 11t – 2t2, where t is measured in hours. They play on a badminton court, which they can rent per hour. Suppose the current price to play on the badminton court is £2.50 per hour. How many hours should Fang play if she wishes to maximise her utility? Explain what we mean by the principle of diminishing marginal utility. Does the principle apply in Fang’s case? Explain why. In a diagram with income in pound sterling on the horizontal axis and quantity on the vertical axis, show the relationship between Fang’s budget and the number of hours that would maximise her consumer surplus.arrow_forwardUse the following information to answer the question below. Cloe is given $4 of pocket money to be spent on either hard candies or chocolates. Chocolates cost 40 cents each and hard candies cost 80 cents each. The marginal utilities derived from the consumption of each product are as shown in the following table. Number of Items Marginal Utility of Chocolates Marginal Utility of Hard Candies 1 60 150 2 50 140 3 40 120 4 30 100 5 20 80 6 10 70 7 5 50 8 0 20 What is Cloe’s total utility at her utility maximizing bundle? Multiple Choice 870 utils 620 utils 80 utils 150 utilsarrow_forward

 Principles of Economics (12th Edition)EconomicsISBN:9780134078779Author:Karl E. Case, Ray C. Fair, Sharon E. OsterPublisher:PEARSON
Principles of Economics (12th Edition)EconomicsISBN:9780134078779Author:Karl E. Case, Ray C. Fair, Sharon E. OsterPublisher:PEARSON Engineering Economy (17th Edition)EconomicsISBN:9780134870069Author:William G. Sullivan, Elin M. Wicks, C. Patrick KoellingPublisher:PEARSON
Engineering Economy (17th Edition)EconomicsISBN:9780134870069Author:William G. Sullivan, Elin M. Wicks, C. Patrick KoellingPublisher:PEARSON Principles of Economics (MindTap Course List)EconomicsISBN:9781305585126Author:N. Gregory MankiwPublisher:Cengage Learning
Principles of Economics (MindTap Course List)EconomicsISBN:9781305585126Author:N. Gregory MankiwPublisher:Cengage Learning Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning
Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning Managerial Economics & Business Strategy (Mcgraw-...EconomicsISBN:9781259290619Author:Michael Baye, Jeff PrincePublisher:McGraw-Hill Education
Managerial Economics & Business Strategy (Mcgraw-...EconomicsISBN:9781259290619Author:Michael Baye, Jeff PrincePublisher:McGraw-Hill Education





