Consider a circular shaped bowl of radius R (see figure 9). A solid ball of mass m and radius r initially lies at the bottom of this bowl. The ball is then given a small push, and the ball then moves to and fro about the bottom of the bowl. At any instant of time, the angle that the ball makes with the vertical is θ (see the figure). a) Find the gravitational potential energy of the ball at any instant of time in terms of m, g, R, and θ. Take the potential energy to be zero at the bottom of the bowl. Assume that θ is small so that cosθ≈1−θ^2/2
Consider a circular shaped bowl of radius R (see figure 9). A solid ball of mass m and radius r initially lies at the bottom of this bowl. The ball is then given a small push, and the ball then moves to and fro about the bottom of the bowl. At any instant of time, the angle that the ball makes with the vertical is θ (see the figure).
a) Find the gravitational potential energy of the ball at any instant of time in terms of m, g, R, and θ. Take the potential energy to be zero at the bottom of the bowl. Assume that θ is small so that cosθ≈1−θ^2/2

consider the ball which is at the bottom of the bowl, when given a small push makes an angle with the vertical. Hence it rises to a height h relative to the initial position.
To find out the potential energy of the ball, consider the initial potential energy of the ball is zero when it is at the bottom of the bowl. Once the ball starts to oscillate, its angular position changes with respect to time.
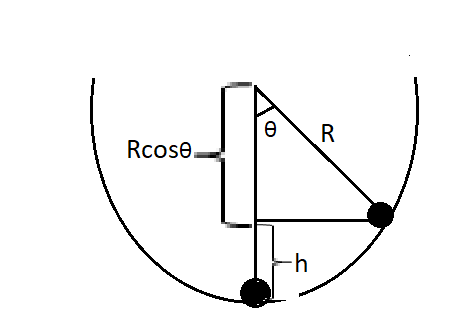
Now the potential energy at any time is dependent on the height of the ball at that time. Consider one such height as shown in the figure, the potential energy of the ball is
Step by step
Solved in 2 steps with 1 images
