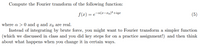
Compute the Fourier transform of the following function: f(x) = e-a(r-x0)²+iqx (5) where a > 0 and q and xo are real. Instead of integrating by brute force, you might want to Fourier transform a simpler function (which we discussed in class and you did key steps for on a practice assignment!) and then think about what happens when you change it in certain ways.

Advance Linear Algebra

Evaluate the following: L-1{ (5s - 2) / (s2 (s + 2)(s - 1)) } ^this is inverse laplace transform

Suppose f(x) - 3x + 4. Compute each of the following. f(6+ 4) = f(6) + f(4) = f(6 – 4) f(6) – f(4) f(6 - 4) = %3D f(6) · f(4) = %3D Submit Question 08 F3 esc F4 F5 3)

i need the answer quickly

See attached picture, and show that (AB)^T = B^T * B^T showing all work and steps, thank you.

7. Describe the transformations of g(x)=-2Vx-1+4 from the base function f(x)=vx.

For two functions, a(x) and b(x), a statement is made that a(x)=b(x) at x=2. What is definitely true about x=2?   1. Both a(x) and b(x) cross the x-axis at 2 or 2. Both a(x) and b(x) have the same output value at x=2

What are the largest possible domains for the following functions: (a) f(x, y) = e√x+y (b) f(x, y) = log(x + √log(y)) (c) f(x, y, z)=√√xyz