Compute the critical value Z2 that corresponds to a 98% level of confidence. Click here to view the standard normal distribution table (page 1). Click here to view the standard normal distribution table (page 2). Zarz (Round to two decimal places as needed.) Standard Normal Distribution Table (page 2) 0.2 333933393553 2223 Ak 0.9 LI 3.0 3.4 2 0,01 0.5040 0.5060 0.5120 05160 05438 05478 05517 DEAN 0.5910 06723 0.664 06985 0.7019 0.7054 0.7257 0.7291 0.73234 0.7357 0.7389 0.7550 0.7611 0.7642 0.7673 0.7704 0.7841 0.7910 0.7939 0.7967 0.7995 0.6591 0.6015 06050 OXIM 0.8159 0.8413 0.8438 0.8643 0.8665 0.3449 03069 0.5000 DEVE 0.5398 0.5793 0.6179 15990 0.9032 09192 0.9332 09452 0.9554 0.5832 0.5871 0.6217 0.6255 0:9049 0:9207 0.06 0.08 0.09 0.5753 0.5239 0.5279 0.5319 0.5359 0.5636 05675 0.5714 0.6006 06301 0.6406 06443 0.6480 0.6517 06736 0.6772 0.6808 0.6544 06141 0.6368 0.7224 0.7088 07123 07422 07454 0.7734 0.7157 0.7190 0.7456 0.7517 0.7549 0.7764 0.7794 0.7823 0.7852 0.8003 0.8078 08133 0.8399 03340 0.8365 0.8599 0.8212 03218 08264 0.3289 03461 03485 0.8508 0.8531 0.8554 0.8577 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8007 0.8925 0.8944 08962 0.9990 08997 0.9147 0.9062 0.9292 0.9418 0.9525 0.9616 0.9082 0.9099 09115 09031 09716 0.9251 0.9365 0:9279 0.9236 0.9370 0.9454 0.9693 0.9699 0.9756 Standard Normal Distribution 0.04 0.05 0.03 82990 0.9222 09345 09357 0.9474 0.9573 1990:0 0.9382 0.9994 09505 0.9495 09564 0.9991 0.9599 09600 09678 09649 0.9671 0.9713 0.9772 09744 0.9750 0.9803 0:9719 0.9726 0.9732 09738 0.9778 09783 09788 0.9793 0.9798 09821 09836 09830 0.9834 0.9838 0.942 0.9846 09861 09864 0.9868 0.9871 0.9675 09881 0990) 0906 0.9998 0.9901 0.9904 0.9906 0.9918 0.9930 0.9922 0.9925 0.9927 0.9918 0.9582 09661 19960 0.5948 0.6331 0.6700 Det ANS anve 0.9940 0.9941 0.9943 0.9945 0.9953 0:9955 0.9956 0.9957 0.9959 0.9965 0.9966 0.9967 0.9968 0.9969 0.9974 0:9975 0.9976 0.9977 0.9977 0.9982 0.9982 0.9983 0.9984 0.9990 0.9991 0.9994 0.9987 0.9987 0.9987 0.9988 09088 0.9991 0.9991 0.9993 0.9993 0.9994 0.9995 0.9997 0.9997 0.9997 0.02 0,00 0.01 0.9997 0.03 0.5506 0.5987 15:08:0 STORO Print 09406 $1360 0.9948 90180 19660 0.8621 0.8830 GWD 0.9015 0.9177 0.9306 0.9319 0.90 09850 0.9884 0.9687 0.9909 0.9911 0.9913 0.9931 09817 0.9857 09890 0.9916 0.9946 0.9960 0.9902 0.9934 0.9936 0.9949 0.9951 0.9952 0.9963 0.990 0:9971 0.9972 0.9973 0.9974 0.9978 0.9979 0.9979 0.9980 0.9964 09985 0.9985 0.99896 0.9986 0.9990 0.9429 09441 0.9535 0.9545 09625 09633 Done 0.9706 0.9763 0.9767 0.9812 15:36:0 0.9993 0.9993 0.9909 0.9989 0.9999 0.9992 0.9992 0.9992 0.9992 0.9994 0.9994 0.9994 0.9995 0.999 0.9995 0.9996 0.9996 0.9996 0.9996 0:9996 0.9997 0.9997 0.9998 0.08 0.09 0.9997 0.04 0.9997 0.9997 0.05 0.06 0.9997 0.07 18660 Standard Normal Distribution Table (page 1) A -3.4 -U -32 -31 -31 -3.0 -29 -2.8 -27 -26 -25 -24 -4 -2.2 -11 -1.8 -1.7 -1.6 -1.5 -14 -13 -12 -1.1 0.0139 0.0136 -2.1 0.0179 0.0174 -2.0 -49 F -86 -45 -0,4 -0.3 7 0.00 0.00003 Standard Normal Distribution 0.01 0,02 0,03 0.04 0,05 0,06 0,07 ILOS 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0005 0.0005 0.0005 0.0004 0.0004 0.0004 0.0004 0.0004 0.0004 0.0006 0.0006 0.0006 0.0009 00013 0.0012 0.09 0.0002 0.0000 0.0009 200 0.0005 0.0005 0.0005 0.0008 0.0008 0.0008 0.0008 0.0007 0.0007 0.0012 0.0011 0.0011 0.0011 0.0000 0.0010 0.0015 0.0014 0.0014 t 0.0021 0.0009 0.0007 0.0007 0.0009 0.0013 0.0013 0.0019 0.0018 0.0018 0.0017 0.0016 0.0016 0.0015 0.0026 0.0025 60004 00003 0.0023 0.0002 0.0021 0.0035 0.0034 0.0003 0.0002 0.0031 6.0000 0.0029 0.0043 0.0041 0.0057 0.0055 0.0078 0.0075 0.0073 0.0002 0.0009 0.0026 0.0047 0.0045 0.0062 0.0002 0.0000 0.0027 0.0040 0.0039 0.0038 0.0037 0.0036 0.0054 0.0052 0.0051 0.0049 0.0048 0.0068 0.0064 0.0009 0.0067 0.0054 0.0071 0.0069 0.0107 0.0096 0.0094 0.0090 00129 0.0125 0.0122 0.0119 0.0116 0.0113 00110 60155 0.0143 0.0188 0.0183 0.0250 0.0044 0.00239 00477 0.0446 0.0436 0.0548 - 0.0537 0.0668 0.0655 0.0008 0.0793 0.0778 0.0681 0.0968 0.0951 0.1151 0.0053 0.008 0.0023 01131 01112 0.1003 0.0985 0.1170 0.0132 0.0170 0.0166 0.0028 0.0222 0.0217 0.0212 0.0287 0.0274 0.0268 0.0062 0.0256 0.0359 0.0336 0.0029 0.0222 0.0314 0.0000 0.0001 2014 0.0418 0.0400 0.0401 0.0302 0.0384 0.0375 00524 0.0516 0.0505 0.0495 0.0455 0.0475 0.0465 0.0643 0.0630 0.0618 0.0606 0.0504 0.0582 0.0571 0.0744 0.0749 0.0735 0.0721 0.0006 0.0918 0.0001 0.0049 0.1093 0.1075 0.1056 0.1038 0.020 0.1357 01335 0.1314 0.1282 0.1271 0.1251 01230 0.1210 0.1190 0.1587 01563 0.1509 01515 03492 01460 01446 0.1423 0.1401 0.1541 01814 01788 01762 01736 01711 01685 02061 02119 0:2090 6.1977 02033 0.2005 0.1999 0.1922 0.1894 02420 02389 0.2358 02327 0.2496 02236 02266 02743 0:2709 02611 0.2546 0.3085 03050 03015 0.2983 0.2946 0.2912 0.2877 Am 0.3372 03446 0.3336 0.3300 0.3364 Aven 0.3821 0.3783 03745 0.3707 03669 0.36.32 0.3504 0.4207 0.4168 0412 0.4000 0.4052 201 0.3974 0.3936 0.3897 04600 0.4562 0.4483 0.4443 0,4404 04364 0.4325 0.4286 0.5000 0.4960 0.480 0.4840 0.4801 0.4760 0.4721 0.03 0.04 0.1379 0.1635 0161 0167 0.2206 0.2177 02148 65% 02514 0.2483 02451 0.2843 02810 02776 01100 03192 0.3156 03121 0.3557 0.3520 03483 03490 04247 04641 0.00 0.01 0.05 0,06 0,07 0.09 2 01000 09000 09000 10000 18:00:0 19:00:0 90000 11000 690000 1920 0,4522 0493 0.02 Print 0.0162 0.0007 $1900 90000 Done 80000 0.0154 00150 0.0197 0.0192 09910 21770 99000 99100 FEITO 0.08 0.0233 0.0094 0.0067 0.0455 0.0559 X
Compute the critical value Z2 that corresponds to a 98% level of confidence. Click here to view the standard normal distribution table (page 1). Click here to view the standard normal distribution table (page 2). Zarz (Round to two decimal places as needed.) Standard Normal Distribution Table (page 2) 0.2 333933393553 2223 Ak 0.9 LI 3.0 3.4 2 0,01 0.5040 0.5060 0.5120 05160 05438 05478 05517 DEAN 0.5910 06723 0.664 06985 0.7019 0.7054 0.7257 0.7291 0.73234 0.7357 0.7389 0.7550 0.7611 0.7642 0.7673 0.7704 0.7841 0.7910 0.7939 0.7967 0.7995 0.6591 0.6015 06050 OXIM 0.8159 0.8413 0.8438 0.8643 0.8665 0.3449 03069 0.5000 DEVE 0.5398 0.5793 0.6179 15990 0.9032 09192 0.9332 09452 0.9554 0.5832 0.5871 0.6217 0.6255 0:9049 0:9207 0.06 0.08 0.09 0.5753 0.5239 0.5279 0.5319 0.5359 0.5636 05675 0.5714 0.6006 06301 0.6406 06443 0.6480 0.6517 06736 0.6772 0.6808 0.6544 06141 0.6368 0.7224 0.7088 07123 07422 07454 0.7734 0.7157 0.7190 0.7456 0.7517 0.7549 0.7764 0.7794 0.7823 0.7852 0.8003 0.8078 08133 0.8399 03340 0.8365 0.8599 0.8212 03218 08264 0.3289 03461 03485 0.8508 0.8531 0.8554 0.8577 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8007 0.8925 0.8944 08962 0.9990 08997 0.9147 0.9062 0.9292 0.9418 0.9525 0.9616 0.9082 0.9099 09115 09031 09716 0.9251 0.9365 0:9279 0.9236 0.9370 0.9454 0.9693 0.9699 0.9756 Standard Normal Distribution 0.04 0.05 0.03 82990 0.9222 09345 09357 0.9474 0.9573 1990:0 0.9382 0.9994 09505 0.9495 09564 0.9991 0.9599 09600 09678 09649 0.9671 0.9713 0.9772 09744 0.9750 0.9803 0:9719 0.9726 0.9732 09738 0.9778 09783 09788 0.9793 0.9798 09821 09836 09830 0.9834 0.9838 0.942 0.9846 09861 09864 0.9868 0.9871 0.9675 09881 0990) 0906 0.9998 0.9901 0.9904 0.9906 0.9918 0.9930 0.9922 0.9925 0.9927 0.9918 0.9582 09661 19960 0.5948 0.6331 0.6700 Det ANS anve 0.9940 0.9941 0.9943 0.9945 0.9953 0:9955 0.9956 0.9957 0.9959 0.9965 0.9966 0.9967 0.9968 0.9969 0.9974 0:9975 0.9976 0.9977 0.9977 0.9982 0.9982 0.9983 0.9984 0.9990 0.9991 0.9994 0.9987 0.9987 0.9987 0.9988 09088 0.9991 0.9991 0.9993 0.9993 0.9994 0.9995 0.9997 0.9997 0.9997 0.02 0,00 0.01 0.9997 0.03 0.5506 0.5987 15:08:0 STORO Print 09406 $1360 0.9948 90180 19660 0.8621 0.8830 GWD 0.9015 0.9177 0.9306 0.9319 0.90 09850 0.9884 0.9687 0.9909 0.9911 0.9913 0.9931 09817 0.9857 09890 0.9916 0.9946 0.9960 0.9902 0.9934 0.9936 0.9949 0.9951 0.9952 0.9963 0.990 0:9971 0.9972 0.9973 0.9974 0.9978 0.9979 0.9979 0.9980 0.9964 09985 0.9985 0.99896 0.9986 0.9990 0.9429 09441 0.9535 0.9545 09625 09633 Done 0.9706 0.9763 0.9767 0.9812 15:36:0 0.9993 0.9993 0.9909 0.9989 0.9999 0.9992 0.9992 0.9992 0.9992 0.9994 0.9994 0.9994 0.9995 0.999 0.9995 0.9996 0.9996 0.9996 0.9996 0:9996 0.9997 0.9997 0.9998 0.08 0.09 0.9997 0.04 0.9997 0.9997 0.05 0.06 0.9997 0.07 18660 Standard Normal Distribution Table (page 1) A -3.4 -U -32 -31 -31 -3.0 -29 -2.8 -27 -26 -25 -24 -4 -2.2 -11 -1.8 -1.7 -1.6 -1.5 -14 -13 -12 -1.1 0.0139 0.0136 -2.1 0.0179 0.0174 -2.0 -49 F -86 -45 -0,4 -0.3 7 0.00 0.00003 Standard Normal Distribution 0.01 0,02 0,03 0.04 0,05 0,06 0,07 ILOS 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0005 0.0005 0.0005 0.0004 0.0004 0.0004 0.0004 0.0004 0.0004 0.0006 0.0006 0.0006 0.0009 00013 0.0012 0.09 0.0002 0.0000 0.0009 200 0.0005 0.0005 0.0005 0.0008 0.0008 0.0008 0.0008 0.0007 0.0007 0.0012 0.0011 0.0011 0.0011 0.0000 0.0010 0.0015 0.0014 0.0014 t 0.0021 0.0009 0.0007 0.0007 0.0009 0.0013 0.0013 0.0019 0.0018 0.0018 0.0017 0.0016 0.0016 0.0015 0.0026 0.0025 60004 00003 0.0023 0.0002 0.0021 0.0035 0.0034 0.0003 0.0002 0.0031 6.0000 0.0029 0.0043 0.0041 0.0057 0.0055 0.0078 0.0075 0.0073 0.0002 0.0009 0.0026 0.0047 0.0045 0.0062 0.0002 0.0000 0.0027 0.0040 0.0039 0.0038 0.0037 0.0036 0.0054 0.0052 0.0051 0.0049 0.0048 0.0068 0.0064 0.0009 0.0067 0.0054 0.0071 0.0069 0.0107 0.0096 0.0094 0.0090 00129 0.0125 0.0122 0.0119 0.0116 0.0113 00110 60155 0.0143 0.0188 0.0183 0.0250 0.0044 0.00239 00477 0.0446 0.0436 0.0548 - 0.0537 0.0668 0.0655 0.0008 0.0793 0.0778 0.0681 0.0968 0.0951 0.1151 0.0053 0.008 0.0023 01131 01112 0.1003 0.0985 0.1170 0.0132 0.0170 0.0166 0.0028 0.0222 0.0217 0.0212 0.0287 0.0274 0.0268 0.0062 0.0256 0.0359 0.0336 0.0029 0.0222 0.0314 0.0000 0.0001 2014 0.0418 0.0400 0.0401 0.0302 0.0384 0.0375 00524 0.0516 0.0505 0.0495 0.0455 0.0475 0.0465 0.0643 0.0630 0.0618 0.0606 0.0504 0.0582 0.0571 0.0744 0.0749 0.0735 0.0721 0.0006 0.0918 0.0001 0.0049 0.1093 0.1075 0.1056 0.1038 0.020 0.1357 01335 0.1314 0.1282 0.1271 0.1251 01230 0.1210 0.1190 0.1587 01563 0.1509 01515 03492 01460 01446 0.1423 0.1401 0.1541 01814 01788 01762 01736 01711 01685 02061 02119 0:2090 6.1977 02033 0.2005 0.1999 0.1922 0.1894 02420 02389 0.2358 02327 0.2496 02236 02266 02743 0:2709 02611 0.2546 0.3085 03050 03015 0.2983 0.2946 0.2912 0.2877 Am 0.3372 03446 0.3336 0.3300 0.3364 Aven 0.3821 0.3783 03745 0.3707 03669 0.36.32 0.3504 0.4207 0.4168 0412 0.4000 0.4052 201 0.3974 0.3936 0.3897 04600 0.4562 0.4483 0.4443 0,4404 04364 0.4325 0.4286 0.5000 0.4960 0.480 0.4840 0.4801 0.4760 0.4721 0.03 0.04 0.1379 0.1635 0161 0167 0.2206 0.2177 02148 65% 02514 0.2483 02451 0.2843 02810 02776 01100 03192 0.3156 03121 0.3557 0.3520 03483 03490 04247 04641 0.00 0.01 0.05 0,06 0,07 0.09 2 01000 09000 09000 10000 18:00:0 19:00:0 90000 11000 690000 1920 0,4522 0493 0.02 Print 0.0162 0.0007 $1900 90000 Done 80000 0.0154 00150 0.0197 0.0192 09910 21770 99000 99100 FEITO 0.08 0.0233 0.0094 0.0067 0.0455 0.0559 X
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
![Compute
Click here to view the standard normal distribution table (page 1).
Click here to view the standard normal distribution table (page 2).
the critical value Zα/2 that corresponds to a 98% level of confidence.
Z«/2 =]
(Round to two decimal places as needed.)
Standard Normal Distribution Table (page 2)
Area
0.00
0.5398
0.00
0.01
0.5040
0.5438
0.3632
0.6501
0.8186
0.01
0.02
Standard Normal Distribution
0.05
0.03
Print
0.04
0.05 0.06
Done
0.07
0.5673
0.7157
0.1400
0.07
0.5319
0.5714
0.0105
0.6844
0.7190
0.7517
0.9986
0.9990
0.9995
0.09
X
Standard Normal Distribution Table (page 1)
0.00
0.01
0.0012
0.01
0.02
Standard Normal Distribution
0.04
0.05
0.02
0.0004
0.001
0.1515
0.176
09237
0.2643
0.2983
0.0004
0.0006
0.001
Print
0.0031
0.0041
0.007
0.1271
0.1492
0.3372 0.3336 0.3300
0.3145 0.3707
0.412 04182
0.4880
0.4920
0.03
0.0003
0.0004
0.0006
0.0011
0.0049
0105
0.0004
0.0006
0.0011
0.1469 0.1446
0.1736
0.1711 0.1685
02206 02266 0.3226 02206
0.2611 0.2578 0.2546 02514
0.2946 0.2912
0.2877 02843
0.3264
0.3669 0.3632
04442 0.4404
0.4840 0.4801
0.04
0.05
Done
0.0029
0.3156
0.3228 0.3192
0.3594 0.5551 0.3520
0.4364 01225
0.4761
0.06
0.2482
0.2810
0.07
0.4286
0.4681
0.08
0.277
1.4641
0.00](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F610adb54-839d-4864-982f-688a650761e4%2Fc5cd4f99-b98b-400f-bf1d-dea619f525a0%2Fkseldl_processed.png&w=3840&q=75)
Transcribed Image Text:Compute
Click here to view the standard normal distribution table (page 1).
Click here to view the standard normal distribution table (page 2).
the critical value Zα/2 that corresponds to a 98% level of confidence.
Z«/2 =]
(Round to two decimal places as needed.)
Standard Normal Distribution Table (page 2)
Area
0.00
0.5398
0.00
0.01
0.5040
0.5438
0.3632
0.6501
0.8186
0.01
0.02
Standard Normal Distribution
0.05
0.03
Print
0.04
0.05 0.06
Done
0.07
0.5673
0.7157
0.1400
0.07
0.5319
0.5714
0.0105
0.6844
0.7190
0.7517
0.9986
0.9990
0.9995
0.09
X
Standard Normal Distribution Table (page 1)
0.00
0.01
0.0012
0.01
0.02
Standard Normal Distribution
0.04
0.05
0.02
0.0004
0.001
0.1515
0.176
09237
0.2643
0.2983
0.0004
0.0006
0.001
Print
0.0031
0.0041
0.007
0.1271
0.1492
0.3372 0.3336 0.3300
0.3145 0.3707
0.412 04182
0.4880
0.4920
0.03
0.0003
0.0004
0.0006
0.0011
0.0049
0105
0.0004
0.0006
0.0011
0.1469 0.1446
0.1736
0.1711 0.1685
02206 02266 0.3226 02206
0.2611 0.2578 0.2546 02514
0.2946 0.2912
0.2877 02843
0.3264
0.3669 0.3632
04442 0.4404
0.4840 0.4801
0.04
0.05
Done
0.0029
0.3156
0.3228 0.3192
0.3594 0.5551 0.3520
0.4364 01225
0.4761
0.06
0.2482
0.2810
0.07
0.4286
0.4681
0.08
0.277
1.4641
0.00
Transcribed Image Text:The following data represent the pH of rain for a random sample of 12 rain dates. A normal probability plot suggests the data could come from a population that is normally
distributed. A boxplot indicates there are no outliers. Complete parts a) through d) below.
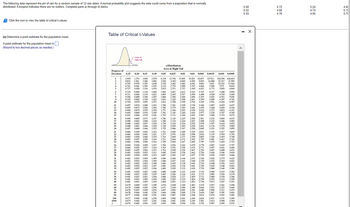
Click the icon to view the table of critical t-values.
(a) Determine a point estimate for the population mean.
A point estimate for the population mean is
(Round to two decimal places as needed.)
Table of Critical t-Values
Degrees of
Freedom
right tail
0.25 0.20 0.15 0.10
3.078
0.816 1.061 1.386 1.886
0.765
0.978 1.250 1.638
0.920 1.156 1.476
t-Distribution
Area in Right Tail
0.02
15.804
4.849
3.482
0.05
6.314 12.706
2.920
2.353
2015
0.01 0.005 0.0025 0.001 0.0005
31.821 63.657 127321 318.309 636.619
6.965 9.925
14.089 22.327 31.599
5.841
7.453 10.215
8610
3.365 4.033
5 802
5.208
4.785
7.201
4.144
4.025
4.773
4.317
C
171
4.56
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 3 images
Similar questions
Recommended textbooks for you
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON
The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman