
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
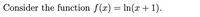
Transcribed Image Text:Consider the function \( f(x) = \ln(x + 1) \).

Transcribed Image Text:**Problem Statement:**
Compute the approximate value of ln(2) using the Taylor polynomials calculated in (a). How large is the approximation error?
---
**Explanation:**
This problem requires you to use Taylor polynomials to approximate the natural logarithm of 2, denoted as ln(2). You should have already calculated the relevant Taylor polynomials in part (a) of your task. Once you have the polynomial approximation of ln(2), you will need to determine the size of the approximation error. This involves comparing the approximation to the actual value of ln(2) and calculating the difference. This exercise is a practical application of Taylor series in approximating functions and assessing accuracy.
Expert Solution
arrow_forward
Step 1
Consider the function,
f(x)=ln(x+1) ⋯⋯(1)
At x=0, equation (1) becomes,
f(0)=ln(0+1)=ln1=0
Taking the derivatives of the function f(x) and using x=0,
f'
arrow_forward
Step 2
The Taylor polynomial of of degree is given by,
Then, the Taylor polynomial of of degree 4 is,
Put in equation (2),
Step by stepSolved in 3 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- How large should the value of (n) such that the Taylor polynomial of order (n) about 100 gives an approximate value for sqrt(101) with an error less than 10-10 in absolute value.arrow_forwardApproximate e2 using a 3rd-degree Taylor Polynomial centered at 0, and determine the maximum error of approximation.arrow_forwardConsider the function f(x) = Vx + I. Compute f'(x) and f"(x). • (a) • (b) ) Write down the Taylor polynomials T1 and T2 of the function f at the point a = 0. • (c) DWhich value of b makes f(b) equal to V1.4? • (d) ) What are the estimates of V1.4 given by Tj and T2 from part (b)? (The actual value of V1.4 is about 1. 1832.)arrow_forward
- Find a formula for Re(z), the remainder for the Taylor polynomial of order 6 based at a = 0 for f(x) = In(7+z) A) Re(x) = 7(7+e) B) Re(x) = 6(7+e)" C) Ro(x) : D) R$(z) = %3D 7(7+e)" 6(7+c)arrow_forwardFind the value of f)(3) if f(x) is approximated near x = 3 by the 10 Taylor polynomial p(x) = f(4) (3) n=0 (x-3)" n!arrow_forward9. Find the Taylor polynomial of degree 3 centered at a = 27 that approximates the function f(x) = Vx. Find a bound on the error in using this polynomial to approximate 27.02arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

