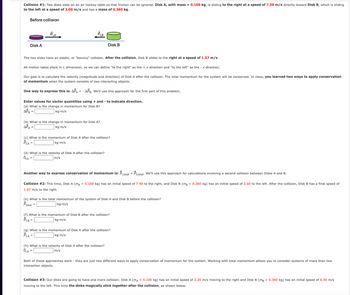
Collision #1: Two disks slide on an air hockey table so that friction can be ignored. Disk A, with mass = 0.100 kg, is sliding to the right at a speed of 7.50 m/s directly toward Disk B, which is sliding to the left at a speed of 3.00 m/s and has a mass of 0.360 kg. Before collision Disk A BA Disk B The two disks have an elastic, or "bouncy" collision. After the collision, Disk B slides to the right at a speed of 1.57 m/s. All motion takes place in 1 dimension, so we can define "to the right" as the +x direction and "to the left" as the -x direction. Our goal is to calculate the velocity (magnitude and direction) of Disk A after the collision. The total momentum for the system will be conserved. In class, you learned two ways to apply conservation of momentum when the system consists of two interacting objects. One way to express this is: APA APB. We'll use this approach for the first part of this problem. Enter values for vector quantities using + and - to indicate direction. (a) What is the change in momentum for Disk B? APB = kg-m/s (b) What is the change in momentum for Disk A? APA = kg.m/s (c) What is the momentum of Disk A after the collision? Pt,A= kg-m/s (d) What is the velocity of Disk A after the collision? Uf,A= m/s Another way to express conservation of momentum is: Pi,total = Pf,total. We'll use this approach for calculations involving a second collision between Disks A and B. Collision #2: This time, Disk A (mA = 0.100 kg) has an initial speed of 7.90 to the right, and Disk B (mB = 0.360 kg) has an initial speed of 2.60 to the left. After the collision, Disk B has a final speed of 1.97 m/s to the right. (e) What is the total momentum of the system of Disk A and Disk B before the collision? Ptotal = kg-m/s (f) What is the momentum of Disk B after the collision? Pf,B = kg-m/s (g) What is the momentum of Disk A after the collision? Pt,A= kg.m/s (h) What is the velocity of Disk A after the collision? Uf,A= m/s Both of these approaches work they are just two different ways to apply conservation of momentum for the system. Working with total momentum allows you to consider systems of more than two interaction objects. Collision #3: Our disks are going to have one more collision: Disk A (mA = 0.100 kg) has an initial speed of 2.20 m/s moving to the right and Disk B (mB = 0.360 kg) has an initial speed of 6.50 m/s moving to the left. This time the disks magically stick together after the collision, as shown below. - Both of these approaches work they are just two different ways to apply conservation of momentum for the system. Working with total momentum allows you to consider systems of more than two interaction objects. Collision #3: Our disks are going to have one more collision: Disk A (mA = 0.100 kg) has an initial speed of 2.20 m/s moving to the right and Disk B (mB moving to the left. This time the disks magically stick together after the collision, as shown below. after collision BLA-B =? Disk A Disk B (i) What is the total momentum of the system? Ptotal kg.m/s (j) What is the velocity of the stuck-together disks after the collision? VA and B m/s = 0.360 kg) has an initial speed of 6.50 m/s

A 2-kg object moving to the right with a speed of 4 m/s makes a head-on, elastic collision with a 1-kg object that is initially at rest. The velocity of the 1-kg object after the collision is (a) greater than 4 m/s, (b) less than 4 m/s, (c) equal to 4 m/s, (d) zero, or (e) impossible to say based on the information provided.

At a bowling alley, two players each score a spare when their bowling balls make head-on, approximately elastic collisions at the same speed with identical pins. After the collisions, the pin hit by ball A moves much more quickly than the pin hit by ball B. Which ball has more mass? Figure CQ6.12

A car of mass 750 kg traveling at a velocity of 27 m/s in the positive x-direction crashes into the rear of a truck of mass 1 500 kg that is at rest and in neutral at an intersection. If the collision is inelastic and the truck moves forward at 15.0 m/s, what is the velocity of the car after the collision? (See Section 6.3.)

A head-on, elastic collision occurs between two billiard balls of equal mass. If a red ball is traveling to the right with speed v and a blue ball is traveling to the left with speed 3v before the collision, what statement is true concerning their velocities subsequent to the collision? Neglect any effects of spin. (a) The red ball travels to the left with speed v, while the blue ball travels to the right with speed 3v. (b) The red ball travels to the left with speed v, while the blue ball continues to move to the left with a speed 2v. (c) The red ball travels to the left with speed 3v, while the blue ball travels to the right with speed v. (d) Their final velocities cannot be determined because momentum is not conserved in the collision. (e) The velocities cannot be determined without knowing the mass of each ball.

A 5-kg cart moving to the right with a speed of 6 m/s collides with a concrete wall and rebounds with a speed of 2 m/s. What is the change in momentum of the cart? (a) 0 (b) 40 kg m/s (c) 40 kg m/s (d) 30 kg m/s (e) 10 kg m/s

A tennis ball of mass 57.0 g is held just above a basketball of mass 500 g as shown in Figure P9.17. With their centers vertically aligned, both balls are released from rest at the same time, to fall through a distance of 1.20 m. (a) Find the magnitude of the downward velocity with which the basketball reaches the ground. (b) Assume that an elastic collision with the ground instantaneously reverses the velocity of the basketball while the tennis ball is still moving down. Next, the two balls meet in an elastic collision. To what height does the tennis ball rebound? Figure P9.17

An estimated force-time curve for a baseball struck by a bat is shown in Figure P9.13. From this curve, determine (a) the magnitude of the impulse delivered to the ball and (b) the average force exerted on the ball. Figure P9.13

If a rainstorm drops 1 cm of rain over an area of 10km2 in the period of 1 hour, what is the momentum of the rain that falls in one second? Assume the terminal velocity of a raindrop is 10 m/s.

The magnitude of the net force exerted in the x direction on a 2.50-kg particle varies in time as shown in Figure P9.10 (page 244). Find (a) the impulse of the force over the 5.00-s time interval, (b) the final velocity the particle attains if it is originally at rest, (c) its final velocity if its original velocity is 2.00im/s, and (d) the average force exerted on the particle for the time interval between 0 and 5.00 s. Figure P9.10