
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Given the data in the image, what would the
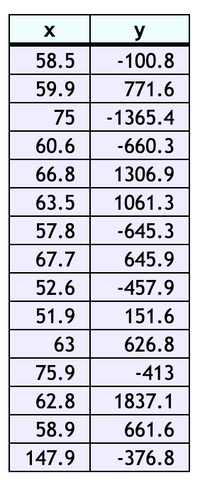
Transcribed Image Text:y
58.5
-100.8
59.9
771.6
75
-1365.4
60.6
-660.3
66.8
1306.9
63.5
1061.3
57.8
-645.3
67.7
645.9
52.6
-457.9
51.9
151.6
63
626.8
75.9
-413
62.8
1837.1
58.9
661.6
147.9
-376.8
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Choose the value of the Pearson's Correlation Coefficient (r) that best describes the two plots. : 0.504, II: -0.232. 2) I: -0.904, II: 0.232. 3) I: 0.904, II: -0.232. 4) I: -0.232, II: 1.304. 5) I: 0.904, II: -0.632.arrow_forwardThe number of wins for a high school football team is measured for the season. When the team plays at home, it is generally believed that they will win. Comparing the location of the game and the number of wins, a correlation coefficient of −0.11 is calculated. What would this imply about the football team winning at home? The scatter plot would closely resemble a straight line with a negative slope. The data has a strong, negative correlation, and a causal relationship exists between the team playing at home and winning. The scatter plot would closely resemble a straight line with a negative slope. The data has a strong, negative correlation, but causation cannot be determined. The scatter plot would not be represented by a line of best fit with a negative slope. There is a weak correlation between the football team playing at home and winning, and a causal relationship exists between the team playing at home and winning. There is no causation and almost no correlation between the…arrow_forwardA researcher measures GPA and height for a group of high school students. What kind of correlation is likely to be obtained for these two variables?arrow_forward
- What effect does an outlier have on a correlation coefficient? Would it increase, decrease or stay the same?arrow_forwardThe Minitab output shown below was obtained by using paired data consisting of weights (in Ib) of 27 cars and their highway fuel consumption amounts (in mi/gal). Along with the paired sample data, Minitab was also given a car weight of 4500 lb to be used for predicting the highway fuel consumption amount. Use the information provided in the display to determine the value of the linear correlation coefficient. (Be careful to correctly identify the sign of the correlation coefficient.) Given that there are 27 pairs of data, is there sufficient evidence to support a claim of linear correlation between the weights of cars and their highway fuel consumption amounts? Click the icon to view the Minitab display. Minitab output The linear correlation coefficient is. (Round to three decimal places as needed.) The regression equation is Highway = 50.4- 0.00535 Weight %3D Predictor Сoef SE Coef T Constant 50.383 2.732 17.75 0.000 Weight - 0.0053502 0.0007856 -7.55 0.000 S= 2.17876 R-Sq = 65.1% R-…arrow_forwardAn ecologist is interested in exploring the relationship between pollination rate and the number of bees present at apple orchards. The relationship is: (Pollination rate) = 372.6 + 13.5 x (bees) with r = 0.80. The best interpretation of the correlation coefficient is: (pick one) 1. 64% of the variability in pollination rate observed at apple orchards is explained by the relationship with the number of bees 2. the correlation between pollination rate and number of bees is 0.64 3. 80% of the variability in number of bees at apple orchards is explained by the relationship with the pollination rate 4. the correlation between pollination rate and number of bees is 0.80arrow_forward
- For a sample of eight bears, researchers measured the distances around the bears' chests and weighed the bears. Minitab was used to find that the value of the linear correlation coefficient is r = 0.862. Using a = 0.05, determine if there is a linear correlation between chest size and weight. What proportion of the variation in weight can be explained by the linear relationship between weight and chest size? Click here to view a table of critical values for the correlation coefficient. a. Is there a linear correlation between chest size and weight? O A. No, because the absolute value of r exceeds the critical value of 0.707. O B. Yes, because r falls between the critical values of -0.707 and 0.707. O C. Yes, because the absolute value of r exceeds the critical value of 0.707. O D. The answer cannot be determined from the given information. b. What proportion of the variation in weight can be explained by the linear relationship between weight and chest size? (Round to three decimal…arrow_forwardThe Minitab output shown below was obtained by using paired data consisting of weights (in lb) of 26 cars and their highway fuel consumption amounts (in mi/gal). Along with the paired sample data, Minitab was also given a car weight of 3000 lb to be used for predicting the highway fuel consumption amount. Use the information provided in the display to determine the value of the linear correlation coefficient. (Be careful to correctly identify the sign of the correlation coefficient.) Given that there are 26 pairs of data, is there sufficient evidence to support a claim of linear correlation between the weights of cars and their highway fuel consumption amounts? Click the icon to view the Minitab display. The linear correlation coefficient is (Round to three decimal places as needed.) Minitab output The regression equation is Highway = 50.3 -0.00539 Weight Predictor Coef SE Coef Constant 50.288 2.998 Weight -0.0053868 0.0007773 |S=2.11773 R-Sq=64.0% R-Sq(adj) = 60.9% Predicted Values…arrow_forwardFifty-four wild bears were anesthetized, and their weights and chest sizes were measured. Results are showing in the graph below. IS there sufficient evidence to support the claim that there is a linear correlation between weights of bears and their chest sizes? When measuring an anesthetized bear, is it easier to measure chest size than weight? If so, does it appear that a measured chest size can be used to predict the weight? Correlation Results Correlation coeff r:0.963141 Critical r ±0.2680855 P-value (two-tailed) 0.000arrow_forward
- Once the correlation coefficient is known, how can we find the amount of the shared variance?arrow_forwardFifty-four wild bears were anesthetized, and then their weights and chest sizes were measured and listed in a data set. Results are shown in the accompanying display. Is there sufficient evidence to support Correlation Results the claim that there is a linear correlation between the weights of bears and their chest sizes? When measuring an anesthetized bear, is it easier to measure chest size than weight? If so, does it appear that Correlation coeff, r: 0.959614 a measured chest size can be used to predict the weight? Use a significance level of = 0.05. Critical r: +0.2680855 P-value (two tailed): 0.000 Но: Р H1:P (Type integers or decimals. Do not round.) Identify the correlation coefficient, r. (Round to three decimal places as needed.) Identify the critical value(s). (Round to three decimal places as needed.) O A. There is one critical value at r= . B. There are two critical values at r= ± Is there sufficient evidence to support the claim that there is a linear correlation between…arrow_forwardIn a study of the stability of IQ scores, a large group of individuals is tested once at age 18 and again at age 35. The following results are obtained. At age 18: average score = 100, SD = 15 At age 35: average score = 100, SD = 15 The correlation coefficient between scores at age 18 and 35 is 0.80 and the scatter plot is football shaped. What percent of the individuals with a score of 115 at age 18 score more than 100 at age 35? Fill in the blank with a number between 0 and 100 to represent the percentage. (Do not enter the % sign.) Don't worry about rounding; any correctly rounded answer will receive full credit.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman