College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
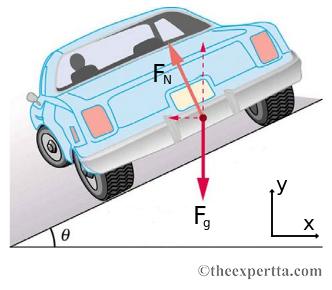
Circular turns of radius r in a race track are often banked at an angle θ to allow the cars to achieve higher speeds around the turns. Assume friction is not present, and use the coordinate system specified.
Part (a) Find the y-component of the normal force FN on a car going around the turn in terms of the angle θ and the magnitude of the normal vector FN.
Part (b) Find the x-component of the normal force FN on a car going around the turn in terms of the angle θ and the magnitude of the normal vector FN.
Part (c) Now write the magnitude of the normal force in terms of the force of gravity Fg and the angle θ.
Part (d) Now write the magnitude of the normal force again, this time in terms of the gravitational force Fg, g, θ, the radius of the track r, and the velocity that the car is traveling at v.
Part (e) Now assume that the car is moving at 15 m/s and the radius of the track is 410 m. What is the angle θ in degrees?
Transcribed Image Text:FN
e
Fg
Otheexpertta.com
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Step 1: Given data
VIEW Step 2: Free-body diagram of given system.
VIEW Step 3: The horizontal and vertical components of normal force.
VIEW Step 4: Calculation for magnitude of normal force in terms of Fg and angle theta.
VIEW Step 5: Calculation for magnitude of normal force in terms of Fg, g, m, r, v and angle theta.
VIEW Step 6: Calculation for the numeric value of angle of inclination.
VIEW Solution
VIEW 
Trending nowThis is a popular solution!
Step by stepSolved in 7 steps with 55 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Chapter 04, Problem 003 GO Two horizontal forces, F, and F,, are acting on a box, but only F, is shown in the drawing. F, The box moves only along the x axis. There is no friction between the box and the surface. Suppose that F = +7.1N and the mass of the box is 3.3 kg. Find the magnitude and direction of F, when the acceleration of the box is (a) +4.7 m/s², (b) -4.7 m/s², and (c) 0 m /s2. can point either to the right or to the left. F, (a) E = (b) F (c) Farrow_forwardCurrent Attempt in Progress Three astronauts, propelled by jet backpacks, push and guide a 100 kg asteroid toward a processing dock, exerting the forces shown in the figure, with F₁ = 27 N, F₂ = 55 N, F3 = 39 N, 0₁ = 30°, and 03 = 60°. What is the (a) magnitude and (b) angle (measured relative to the positive direction of the x axis in the range of (-180°, 180°]) of the asteroid's acceleration? (a) Number i (b) Number Units Units Fy Rarrow_forwardF(t) Force_Crate Known values: Mass of Block 68 kg TT Hs μk 0 0.63 0.53 26° Problem Statement: A crate is initially at rest on a sloped surface, when a force is applied: F(t) where t is in seconds. Answers: When t=44.47 seconds, the crate has not yet started moving. Find the magnitude of the friction force at that time: 317.771 N The direction of the friction force at that time is: down the slope Find the time required for the crate to start moving: Find the crate's speed when t=174.9 s: 9.485 m/s Be sure to include units with your answers. 169.756 S 240+0.2 N,arrow_forward
- answer c pleasearrow_forwardA cougar bites a llama of mass m and drags it across some rough horizontal ground. The cougar applies a horizontal force of magnitude F, and the llama is dragged at a constant velocity. The coefficient of kinetic friction is μk. While the cougar applies the force F, the magnitude of the kinetic friction force, fk , on the llama obeys: a)F > µk m g > fk b)F = fk = µk m gc)F = fk < µk m gd)cannot answer, not enough information givene) F > fk = µk m garrow_forwardA 2.00-kg block is placed on top of a 5.00-kg block. The coefficient of kinetic friction between the 5.00-kg block and the surface is 0.200. A horizontal force F is annlied to the 5.00-kg block. m g=9.8 (a) Draw FBD for each block. (b) Find force F that makes both blocks moving to the right with a = 3.0 m/s² 2.00 kg 2 (C) Find the coefficient of static friction between both blocks that prevents the 2.00-kg block to slide down when both blocks is moving with a = 3.0 m/s² 5.00 kg S Farrow_forward
- A woman exerts a horizontal force of 111 N on a box with a mass of 31.7 kg. HINT (a) If the box doesn't move, what's the magnitude of the static friction force (in N)? N (b) What is the minimum possible value of the coefficient of static friction between the box and the floor? (Assume the box remains stationary.)arrow_forwardThe 118-lb force P is applied to the 250-lb crate, which is stationary before the force is applied. Determine the magnitude and direction of the friction force F exerted by the horizontal surface on the crate. The friction force is positive if to the right, negative if to the left. Assume ??= 0.48, ??= 0.38.arrow_forwardA 2.5 kg mass is initially at rest on a horizontal surface. An applied force acts in the +x direction resulting in a displacement of 1.50 m. If the speed of the mass is 4.00 m/s at the 1.50 m mark and the applied force is 22.0 N, what is the coefficient of kinetic friction?arrow_forward
- Block A in the figure has mass mA = 4.20 kg, and block B has mass mg = 2.00 kg. The coefficient of kinetic friction between block B and the horizontal plane is k = 0.500. The inclined plane is frictionless and at angle = 30.0°. The pulley serves only to change the direction of the cord connecting the blocks. The cord has negligible mass. Find (a) the tension in the cord and (b) the magnitude of the acceleration of the blocks. Frictionless, massless pulley MA mp Barrow_forwardA girl exerts a horizontal force of 133 N on a box with a mass of 33.2 kg. (a) If the box doesn't move, what's the magnitude of the static friction force (in N)? N (b) What is the minimum possible value of the coefficient of static friction between the box and the floor? (Assume the box remains stationary.)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press 
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON
Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON