
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question

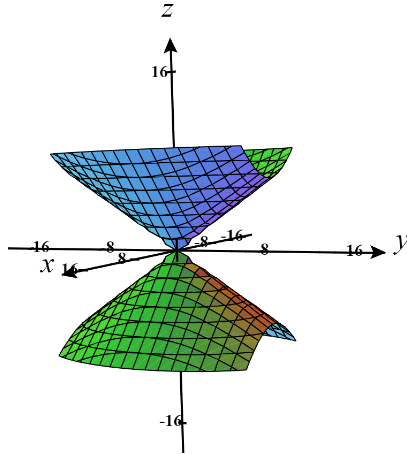
Transcribed Image Text:(a) Circle the equation that generates the surface shown below.
*The image shows a 3D graph of a hyperbolic paraboloid. This surface is a saddle-shaped figure that extends infinitely.*
Equations to choose from:
a) \( y - z^2 = 0 \)
b) \( 2x + 3y - z = 5 \)
c) \( 4x^2 + \frac{y^2}{2} + z^2 = 9 \)
d) \( x^2 + \frac{y^2}{2} - z^2 = 9 \)
e) \( x^2 + \frac{y^2}{2} = z^2 \)
f) \( x^2 + \frac{z^2}{2} - y^2 = 9 \)
g) \( z^2 + \frac{y^2}{2} = x^2 \)
h) \( z = x^2 - y^2 \)
i) \( 9 = z^2 + y^2 \)
*See next page for part (b)*
The graph is color-coded, with green and orange portions indicating the different sections of the saddle surface. The axes are labeled as \( x \), \( y \), and \( z \).

Transcribed Image Text:**Contour Map Sketching**
**Problem 9(b):**
Given the function \( f(x, y) = 2x - y \), sketch a well-labeled contour map for the contour levels \( z_0 = 0, 1, 2, 3 \).
---
### Explanation
In the image, there is a grid provided for sketching the contour map. To create a contour map for the given function \( f(x, y) = 2x - y \), follow these steps:
1. **Contour Lines:**
For each contour level \( z_0 \), set the equation \( f(x, y) = z_0 \).
- For \( z_0 = 0 \):
\( 2x - y = 0 \) → \( y = 2x \)
- For \( z_0 = 1 \):
\( 2x - y = 1 \) → \( y = 2x - 1 \)
- For \( z_0 = 2 \):
\( 2x - y = 2 \) → \( y = 2x - 2 \)
- For \( z_0 = 3 \):
\( 2x - y = 3 \) → \( y = 2x - 3 \)
2. **Sketching:**
Using the grid, plot each line based on the equations derived for each \( z_0 \). These lines will be linear and parallel since they have the same slope (2).
3. **Labeling:**
Clearly label each line with its respective \( z_0 \) value for clarity.
By sketching these lines on the provided grid, a contour map representing different elevation levels (z-values) for the function can be visualized.
Expert Solution
arrow_forward
Step 1
Solution for 9 (a):
The equation that generates the given graph is choice (e):
x2+y22=z2
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

