Calculate the velocity of the car at the end of the ramp just before it starts its horizontal path to its stopping point. PE = KE = (1/2) m v^2
Displacement, Velocity and Acceleration
In classical mechanics, kinematics deals with the motion of a particle. It deals only with the position, velocity, acceleration, and displacement of a particle. It has no concern about the source of motion.
Linear Displacement
The term "displacement" refers to when something shifts away from its original "location," and "linear" refers to a straight line. As a result, “Linear Displacement” can be described as the movement of an object in a straight line along a single axis, for example, from side to side or up and down. Non-contact sensors such as LVDTs and other linear location sensors can calculate linear displacement. Non-contact sensors such as LVDTs and other linear location sensors can calculate linear displacement. Linear displacement is usually measured in millimeters or inches and may be positive or negative.
I performed a lab using a toy car to go down a ramp that was positioned at different heights. For expample: ramp height = 40 cm, ramp length = 121.92 cm, time car took to clear the ramp from start = .86 seconds, distance car traveled from end of ramp to stopping point = 937.26 cm, mass of car = .54 kg, based off this information.....
Calculate the velocity of the car at the end of the ramp just before it starts its horizontal path to its stopping point. PE = KE = (1/2) m v^2
As per the conservation law of energy,
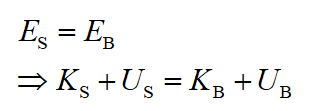
Here, E, K, and U represent the car’s total energy, the car’s kinetic energy, and the car’s potential energy, respectively.
Here, the subscript S and B represent the car’s position at the ramp’s top and ramp’s bottom, respectively.
The car’s kinetic energy can be represented as,
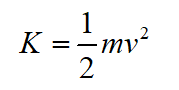
Here, m and v represent the car’s mass and the car’s velocity, respectively.
The car’s potential energy can be represented as,
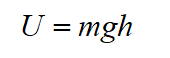
Here h represents the car’s height from the ramp’s bottom.
Step by step
Solved in 2 steps with 5 images
