College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Topic Video
Question
For two existing torques, what third force at a given distance from the pivot will balance them?
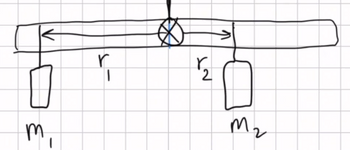
Imagine a meter stick set up as in the figure. It hangs from a central bracket, and two hanging masses can hang from it from each of their brackets. At a third location, a force probe can either pull up or pull down on the stick, depending on what is needed to balance the stick.
The mass of the meter stick is 120 g.
sketch the situation (drawing r1, r2, r3, F1, F2, and F3) and determine the magnitude (value) and direction (+ or -) of each torque. Don't include the mass of a bracket that would hold the hanging mass in place; assume the mass listed is the entire mass hanging at that point.
For each trial, use the principle of equilibrium (where the sum of torques is zero) to calculate the third, unknown force acting at x3
Transcribed Image Text:Trial
1
m₂ (g)
50
x₁ (cm)
20
m₂ (g)
100
x₂ (cm)
80
X3 (cm)
60
fulcrum location (cm)
50
Minimum
measured F3 (N)
1.32
Maximum
measured F3 (N)
1.55
Transcribed Image Text:m
1
r
I
r
2
V
M₂
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
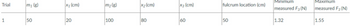
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- In the figure, three forces of the same magnitude are applied to a particle at the origin (acts directly into the plane of the figure). Rank the forces according to the magnitudes of the torques they create about the point P2, greatest first. T1, T2 and T3 are the corresponding torques for forces 1, 2 and 3. Ps P2 F1 O T2 = T3 > T1 O T1 > T2 > T3 O T1 = T2 > T3 T2 T3 > T1 T3 > T2 > T1arrow_forwardA person bending forward to lift a load "with his back" (Figure a) rather than "with his knees" can be injured by large forces exerted on the muscles and vertebrae. The spine pivots mainly at the fifth lumbar vertebra, with the principal supporting force provided by the erector spinalis muscle in the back. To see the magnitude of the forces involved, and to understand why back problems are common among humans, consider the model shown in Figure b, of a person bending forward to lift a Wo = 195-N object. The spine and upper body are represented as a uniform horizontal rod of weight W₁ = 305 N pivoted at the base of the spine. The erector spinalis muscle, attached at a point two-thirds of the way up the spine, maintains the position of the back. The angle between the spine and this muscle is 12.0⁰. Back muscle R₂ T 12.0° 1T Rx Pivot a Wb Wo ..(a).Find the tension in the back muscle. 1.114 Enter a number. differs from the correct answer by more than 10%. Double check your calculations. kN…arrow_forwardA traffic light hangs from a 7.2-m long beam (AB) that is attached to a pole by a hinge (A), as shown. A horizontal (massless) cable (CD) supports the beam, making a 37° angle. The cable is attached to the pole 3.8 m above the hinge. The mass of the beam is 12 kg, and the mass of the traffic light is 22 kg. What is the tension in the cable? Also, the hinge exerts a force— with both horizontal and vertical components— on the beam. Find the magnitude of this force.arrow_forward
- The large quadriceps muscle in the upper leg terminates at its lower end in a tendon attached to the upper end of the tibia (see Figure a). The forces on the lower leg when the leg is extended are modeled as in Figure b, where T is the force of tension in the tendon, w is the force of gravity acting on the lower leg, and F is the force of gravity acting on the foot. Find T when the tendon is at an angle of 25.0° with the tibia, assuming that w = 29.O N, F = 12.3 N, and the leg is extended at an angle 6 of 40.0° with the vertical. Assume that the center of gravity of the lower leg is at its center and that the tendon attaches to the lower leg at a point one-fifth of the way down the leg. (Give the magnitude.) Quadriceps - Tendon Tibia 25.0°7arrow_forwardQuestion is attachedarrow_forwardA 10.6 m long uniform ladder that weighs 428 N is resting against a very slimy wet moss covered wall that can be considered to be frictionless, as shown in the figure below. A firefighter that weighs 785 N is 4.64 meters up the ladder. The ladder is in static equilibrium. The normal force that the ground exerts on the ladder is? (enter your answer with three significant figures)arrow_forward
- Marcel is helping his two children, Jacques and Gilles, to balance on a seesaw so that they will be able to make it tilt back and forth without the heavier child, Jacques, simply sinking to the ground. Given that Jacques, whose weight is W, is sitting at distance L to the left of the pivot, at what distance L1 should Marcel place Gilles, whose weight is w, to the right of the pivot to balance the seesaw? (figure 1) Part A) Express your answer in terms of L, W, and w. Part B) Now consider this problem as a more formal introduction to torque. The torque of each child about the pivot point is the product of the child's weight and the distance from the pivot to the child's center of mass (center of gravity.) The sign of the torque is taken to be positive by convention if it would cause a counterclockwise rotation of the seesaw. The distance is measured perpendicular to the line of force and is called the moment arm. (figure 1) Find the torque τ about the pivot due to the…arrow_forwardLook at the picturearrow_forwardYou push on a rectangular door at the location of the knob (see diagram for top view). The door s mass is 72.4 kg, and its side-to-side width is 2.43 m. The knob is located 0.17 m from the right-hand side of the door. If you push with a force of 124 N, what will the be the door s angular acceleration as it swings on its hinges? (Note: the moment of inertia of the door of mass M and width x, swinging on its hinges, is (1/3) M x^2.) 1.58 rad/s^2 2.76 rad/s^2 1.26 rad/s^2 1.97 rad/s^2arrow_forward
- Can you draw a free-body diagram of this problem? Three children are trying to balance on a seesaw, which includes a fulcrum rock acting as a pivot at the center, and a very light board 3.2 m long as shown in the figure. Two playmates are already on either end. Boy A has a mass of 45 kg, and boy B a mass of 35 kg. Where should girl C, whose mass is 25 kg, place herself so as to balance the seesaw?arrow_forwardYou push on a rectangular door at the location of the knob (see diagram for top view). The door s mass is 70.7 kg, and its side-to-side width is 1.91 m. The knob is located 0.11 m from the right-hand side of the door. If you push with a force of 141 N, what will the be the door s angular acceleration as it swings on its hinges? (Note: the moment of inertia of the door of mass M and width x, swinging on its hinges, is (1/3) M x^2.)arrow_forwardIf the distance h is 1.52 m , what is the vertical component of the force exerted on the wheel A by the track? If the distance h is 1.52 m , what is the vertical component of the force exerted on the wheel B by the track? Find the maximum value h can have without causing one wheel to leave the track. Thank you!arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press 
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON
Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON