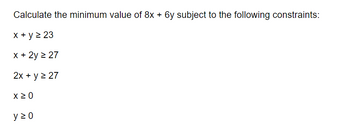
Calculate the minimum value of 8x + 6y subject to the following constraints: x + y ≥ 23 x + 2y ≥ 27 2x + y ≥ 27 x ≥ 0 y≥0

Find the minimum value of the function z = 3x+ 11 y subject to the following constraints. x≤11 y≤ 12 3x+y≥18 3x+7y254 Note that the ALEKS graphing calculator can be used to make computations easier. Z = X 08

The equality lines for the following constraints are shown in the graph below: 40x + 15y 120 25x + 40y < 200 -За + 12у 12 y 5 4 2 F 1. 4. 5 6. 7 8. The feasible region is the area represented by the letter A BCDE F G VI VI VI 3.

Consider the following minimum problem: Minimize: C = 2x₁ + 3x₂ Subject to the constraints: x1 + x₂ > 2 2x1 + 3x₂ ≥ 6 x1 ≥ 0 x₂ > 0 Write the dual problem for the above minimum problem by selecting the appropriate number for each blank box shown below (Do not solve the dual problem). Y₁+ [Select] P [Select] = [Select] [Select] Y₁ ≥ 0 Minimum value of C = Value of 1 = Y2 ≥ 0 Value of 2 = Subject to the constraints: 3x1 + x₂ ≥ 6 -4x1 + 2x₂ ≥ 2 x₁ ≥0 X₂ ≥0 Use the simplex method to solve the following minimum problem on your own paper. Then, using your final tableau, enter the answer in each relevant box provided below. Minimize: C = 3x₁ +4x2 Subject to the following constraints: 2x1 + x₂ > 2 2x1 + x₂ ≥ 6 x₁ ≥ 0 ; x₂ > 0 x1 = Y₁+ X2 = Yı+ C = [Select] [Select] Use the simplex method and the Duality Principle to solve the following minimum problem: Minimize: C = 2x1 + 2x₂ Y2 Y22 y2 ≤ 3 and using your final tableau answer the questions below by entering the correct answer in each blank box.…