ENGR.ECONOMIC ANALYSIS
14th Edition
ISBN: 9780190931919
Author: NEWNAN
Publisher: Oxford University Press
expand_more
expand_more
format_list_bulleted
Related questions
Question
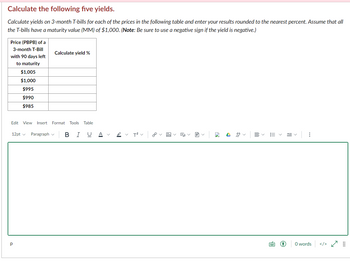
Transcribed Image Text:Calculate the following five yields.
Calculate yields on 3-month T-bills for each of the prices in the following table and enter your results rounded to the nearest percent. Assume that all
the T-bills have a maturity value (MM) of $1,000. (Note: Be sure to use a negative sign if the yield is negative.)
Price (PBPB) of a
3-month T-Bill
with 90 days left
to maturity
$1,005
$1,000
$995
$990
$985
Edit
12pt ✓
Р
View Insert Format Tools Table
B I U
Calculate yield %
Paragraph
A
T² V
Bo
B
DAV
Ill
!!!
⠀
0 words
</> ✓✓
Transcribed Image Text:Understanding the price of bonds and interest rates.
The remarkable thing about the events described in the article is that the yield on the 3-month T-bill was briefly negative. To see how this
could happen, consider the relationship between bond prices and bond yields.
A 3-month T-bill with a maturity value of $1,000 is just a piece of paper that entitles the holder to $1,000 in three months. For example, if you
were to buy a 3-month T-bill on September 24, 2008, with a maturity value of $1,000 and 90 days left to maturity, the U.S. government would
pay you $1,000 on December 23, 2008.
In general, the price of a bond is less than its maturity value. That is, if you are going to give up a certain amount of money for the duration of
the bond, you expect to be paid for this loss of liquidity and compensated for inflation that could reduce the value of the repayment at the
end of the period. Therefore, a piece of paper entitling you to $1,000 on December 23 would usually be worth less than $1,000 on September
24. The yield on a bond is a function of the percent by which your money implicitly grows while invested in it. In order to compare yields
among bonds, yield is always reported as an annual interest rate. A bond's yield is a function of its maturity value (MM), its price (PBPB), and
the number of days until it matures. The general formula for the yield on a zero-coupon bond such as a T-bill is as follows:
Percentage Yield = 100 x
5
1000
= 100 x 0.005 × 4 = 2%
M-PB
M
x 4
For example, if you were to pay $995 for a T-bill maturing in 90 days with a face value of $1,000, the percentage yield would be calculated as
follows:
M = face value of the bond = $1,000
PBM = pay for a T-bill = $995
days to maturity = 90
Percentage Yield = 100 x
= 100 x
X
1000-995
1000
360
days to maturity
360
90
=
Calculate the following five vields.
2%
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 5 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, economics and related others by exploring similar questions and additional content below.Similar questions
- What is the amount of the quarterly deposits A such that you will be able to withdraw the amounts shown in the cash flow diagram if the interest rate is 9% compounded quarterly? The amount of the quarterly deposits A should be $. ( Round to the nearest dollar.) What is the amount of the quarterly deposits A such that you will be able to withdraw the amounts shown in the cash flow diagram if the interest rate is 9% compounded quarterly? 0 A 9% Compounded quarterly $1,300 1 1 The amount of the quarterly deposits A should be S. (Round to the nearest dollar.) 2 4 (Deposit) Quarters 6 7 $3,000 8 Q 2arrow_forwardCalculate the total interest earned, if you save $68 each month, Starting today, for 11 more years, if the annual interest rate is 9.6 and interest is compounded on a monthly basis?arrow_forwardA cash flow at time zero (now) of $14,551 is equivalent to another cash flow that is an EOY annuity of $2,700 over seven years (starting at year 1). Each of these two cash-flow series is equivalent to a third series, which is a uniform gradient series. What is the value of G for this third series over the same seven-year time interval? Assume that the cash flow at the end of year one is zero. ..... Choose the correct answer below. A. $989 B. $785 C. $392 D. $1,450 O E. Not enough information given.arrow_forward
- You are going to borrow $30,000 to purchase a car. You agree to repay the loan in 36 monthly payments of $996.43 each. What is the nominal interest rate (APR) of this loan if interest is being compounded monthly?arrow_forwardYou deposit $100 now, and another $100 at the end of 20 years. The account earns a nominal discount rate of 4% compounded monthly for the first 20 years, and a nominal discount rate of d(52) compounded weekly thereafter. If the account has $700 at the end of 40 years then find this nominal discount rate compounded weekly.arrow_forwardWould love the help.arrow_forward
- 3.2 Compare the interest earned by $1,000 for five years at 8% simple interest with that earned by the same amount for five years at 8% compounded annually. 3.3 You are considering investing $3,000 at an interest rate of 8% compounded annu- ally for five years or investing the $3,000 at 9% per year simple interest for five years. Which option is better?arrow_forwardIf the interest rate is 7.0%, what is the present value of a perpetuity paying $210 per year? (A perpetuity is a bond that makes payments forever.) Round to the nearest dollar. Do not use dollar signs or commas in your answer. Example: if the answer is $1,234.56, then write "1235"arrow_forwardWhat sum deposited today at 9% compounded annually for 18 years will provide the same amount as $2100 deposited at the end of each year for 18 years at 8% compounded annually? What sum would have to be deposited today at 9% interest compounded annually? $ (Round to the nearest cent.)arrow_forward
- Maria deposits $1,300 in a savings account that pays interest at an annual compound rate of 4.0%. Two years after the deposit, the interest rate increases to 5.0% compounded annually. A second deposit of $2,700 is made immediately after the interest rate changes to 5.0%. How much will be in the fund 7 years after the second deposit? $ Round your final answer to 2 decimal places, e.g. 52.75. The cell tolerance is ±0.03arrow_forwardSuppose you borrow $5,000 at 7.25% interest for 14 months. What is the maturity value?arrow_forwardAssume that a 24-month CD purchased for $3000 pays an APY of 4.25% (and of course interest is compounded). How much do you have at maturity? (Round your answer to the nearest cent.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Economics (12th Edition)EconomicsISBN:9780134078779Author:Karl E. Case, Ray C. Fair, Sharon E. OsterPublisher:PEARSON
Engineering Economy (17th Edition)EconomicsISBN:9780134870069Author:William G. Sullivan, Elin M. Wicks, C. Patrick KoellingPublisher:PEARSON
Principles of Economics (MindTap Course List)EconomicsISBN:9781305585126Author:N. Gregory MankiwPublisher:Cengage Learning
Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning
Managerial Economics & Business Strategy (Mcgraw-...EconomicsISBN:9781259290619Author:Michael Baye, Jeff PrincePublisher:McGraw-Hill Education
Principles of Economics (12th Edition)
Economics
ISBN:9780134078779
Author:Karl E. Case, Ray C. Fair, Sharon E. Oster
Publisher:PEARSON
Engineering Economy (17th Edition)
Economics
ISBN:9780134870069
Author:William G. Sullivan, Elin M. Wicks, C. Patrick Koelling
Publisher:PEARSON
Principles of Economics (MindTap Course List)
Economics
ISBN:9781305585126
Author:N. Gregory Mankiw
Publisher:Cengage Learning
Managerial Economics: A Problem Solving Approach
Economics
ISBN:9781337106665
Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike Shor
Publisher:Cengage Learning
Managerial Economics & Business Strategy (Mcgraw-...
Economics
ISBN:9781259290619
Author:Michael Baye, Jeff Prince
Publisher:McGraw-Hill Education