
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
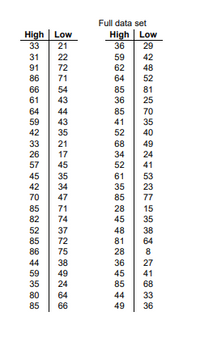
Transcribed Image Text:**Data Table: High and Low Values**
This table presents a data set with two columns of high and low values. The data is split into two sections.
**Section 1:**
- **High Values:** 33, 31, 91, 86, 66, 61, 64, 59, 42, 33, 31, 26, 57, 45, 42, 70, 47, 53, 82, 85, 65, 85, 44, 39, 55, 59, 80, 85
- **Low Values:** 21, 22, 72, 71, 54, 43, 44, 41, 35, 34, 27, 21, 45, 36, 34, 35, 35, 71, 74, 72, 35, 72, 38, 36, 86, 45, 64, 66
**Section 2:**
- **High Values:** 36, 59, 62, 64, 85, 63, 71, 59, 68, 24, 40, 52, 35, 86, 85, 61, 36, 72, 30, 71, 81, 26, 85, 40, 28, 44, 43, 49
- **Low Values:** 29, 42, 48, 52, 34, 25, 85, 35, 49, 23, 31, 44, 75, 77, 35, 8, 72, 8, 21, 68, 44, 27, 36, 68, 45, 36, 33, 36
This data can be utilized for analyzing patterns, computing averages, or any statistical operations suitable for educational purposes.
![A random sample of 50 cities have the data on average high and low temperatures in January shown in the accompanying table. Use the technology of your choice and the given data to complete parts (a) through (f). Use high temperature as the explanatory variable.
[Icon for viewing the table of average high and low temperatures]
**c. Determine and interpret the regression equation for the data. Select the correct choice below and, if necessary, fill in any answer boxes within your choice.**
- **A.** The regression equation is \( \hat{y} = \Box + (\Box)x \), which means there is a positive linear relationship between high and low temperatures.
*(Round to three decimal places as needed.)*
- **B.** The regression equation is \( \hat{y} = \Box + (\Box)x \), which means there is a negative linear relationship between high and low temperatures.
*(Round to three decimal places as needed.)*
- **C.** This question is not applicable since a regression line is not reasonable.](https://content.bartleby.com/qna-images/question/f534fa3a-7fc6-4517-a79f-1e1d7853b104/30c72176-b8be-41c8-85a3-0da4a85448e9/4ug6pt_thumbnail.png)
Transcribed Image Text:A random sample of 50 cities have the data on average high and low temperatures in January shown in the accompanying table. Use the technology of your choice and the given data to complete parts (a) through (f). Use high temperature as the explanatory variable.
[Icon for viewing the table of average high and low temperatures]
**c. Determine and interpret the regression equation for the data. Select the correct choice below and, if necessary, fill in any answer boxes within your choice.**
- **A.** The regression equation is \( \hat{y} = \Box + (\Box)x \), which means there is a positive linear relationship between high and low temperatures.
*(Round to three decimal places as needed.)*
- **B.** The regression equation is \( \hat{y} = \Box + (\Box)x \), which means there is a negative linear relationship between high and low temperatures.
*(Round to three decimal places as needed.)*
- **C.** This question is not applicable since a regression line is not reasonable.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Different hotels in a certain area are randomly selected, and their ratings and prices were obtained online. Using technology, with x representing the ratings and y representing price, we find that the regression equation has a slope of 135 and a y-intercept of -373. Complete parts (a) and (b) below. a. What is the equation of the regression line? Select the correct choice below and fill in the answer boxes to complete your choice. O A. y=] + ()& OB. -+x O D. y=+ ()× b. What does the symbol y represent? O A. The symbol y represents the average price of hotels in the area O B. The symbol y represents the expected price when the hotel's rating is 0. O C. The symbol y represents the predicted value of price. O D. The symbol y represents the amount that price increases with a 1-point increase in rating.arrow_forwardb. What does the symbol y represent? O A. The symbol y represents the predicted value of price. O B. The symbol y represents the amount that price increases with a 1-point increase in rating. O C. The symbol y represents the expected price when the hotel's rating is 0. O D. The symbol y represents the average price of hotels in the area.arrow_forwardDifferent hotels in a certain area are randomly selected, and their ratings and prices were obtained online. Using technology, with x representing the ratings and y representing price, we find that the regression equation has a slope of 120 and a y-intercept of - 369. Complete parts (a) and (b) below. a. What is the equation of the regression line? Select the correct choice below and fill in the answer boxes to complete your choice. O A. A. V= O B. y = O C. ý= O D. y =arrow_forward
- Please solve what’s not filled in.arrow_forwardPlease help ))()()arrow_forwardThe table shows the amounts of crude oil (in thousands of barrels per day) produced by a certain country and the amounts of crude oil (in thousands of barrels per day) imported by the same country for seven years. The equation of the regression line is y =-1.364x+17,178.20. Complete parts (a) and (b) below. Produced, x Imported, y 5,744 5,554 5,439 5,188 5,136 5,067 D 9,132 9,677 10,017 10,193 10,149 10,075 5,756 9,328 (a) Find the coefficient of determination and interpret the result. (Round to three decimal places as needed.)arrow_forward
- The arm span and foot length were both measured (in centimeters) for each of 20 students in a biology class. The computer output displays the regression analysis. Which of the following is the best interpretation of the coefficient of determination r2? About 37% of the variation in arm span is accounted for by the linear relationship formed with the foot length. About 65% of the variation in foot length is accounted for by the linear relationship formed with the arm span. About 63% of the variation in arm span is accounted for by the linear relationship formed with the foot length. About 63% of the variation in foot length is accounted for by the linear relationship formed with the arm span.arrow_forwardUse the given data set to answer parts (a) and (b). a. Find the regression equation for the data points. X 5 b. Graph the regression equation and the data points. y -1 10 -10 y B. 10 -10- C. a. Find the regression equation for the data points. ŷ-0 (Use integers or decimals for any numbers in the expression. Round to two decimal places as needed.) b. Graph the regression equation and the data points. O A. 10 T -10- 1 2 -1 3 327 D. -10 4 y 4 28 0arrow_forwardFill in the blank. Given a collection of paired sample data, the Given a collection of paired sample data, the y=bo+b,x algebraically describes the relationship between the two variables, x and y. y=bo+b₁x algebraically describes the relationship between the two variables, x and y. intercept of probability equation slope of regression equationarrow_forward
- The table shows the amounts of crude oil (in thousands of barrels per day) produced by a certain country and the amounts of crude oil (in thousands of barrels per day) imported by the same country for seven years. The equation of the regression line is y = - 1.269x + 16,635.60. Complete parts (a) and (b) below. Produced, x Imported, y 5,718 5,612 5,409 5,228 5,128 5,006 O 9,106 9,631 10,000 10,140 10,133 10,059 5,759 9,318 (a) Find the coefficient of determination and interpret the result. (Round to three decimal places as needed.)arrow_forwarda. Using the pairs of values for all 10 points, find the equation of the regression line. b. After removing the point with coordinates (2,3), use the pairs of values for the remaining 9 points and find the equation of the regression line. c. Compare the results from parts (a) and (b).arrow_forwardUsing the weights (Ib) and highway fuel consumption amounts (mi/gal) of the 48 cars listed in the accompanying data set, one gets this regression equation: y = 58 9-0.00749x, where x represents weight Complete parts (a) through (d). Click the icon to view the car data. 東 b. What are the specific values of the slope and y-intercept of the regression line? O A. The slope is 58.9 and the y-intercept is 0.007499. B. The slope is -0.00749 and the y-intercept is 58.9. O C. The slope is 58.9 and the y-intercept is -0.00749. O D. The slope is 0.00749 and the y-intercept is 58.9. c. What is the predictor variable? O A. The predictor variable is highway fuel consumption, which is represented by x. B. The predictor variable is weight, which is represented by x. O C. The predictor variable is weight, which is represented by y O D. The predictor variable is highway fuel consumption, which is represented by y. d. Assuming that there is a significant linear correlation between weight and highway fuel…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman

MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc

Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning

Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning

Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON

The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman