MATLAB: An Introduction with Applications
MATLAB: An Introduction with Applications
6th Edition
ISBN: 9781119256830
Author: Amos Gilat
Publisher: John Wiley & Sons Inc
Bartleby Related Questions Icon

Related questions

Q: A car company claims that its new SUV gets better gas mileage than its competitor’s SUV. A random…
A: Company's SUVSample size, Sample mean, Population standard deviation, New SUVSample size, Sample…
Q: The Pew Internet and American Life Project surveyed 2227 adults in 2011, asking them about their…
A: It is given that the mean number of text messages sent per day is 40.9 for men, 42.0 for women. The…
Q: For a population With a mean of 75 and a standard deviation of 12, what is the probability that a…
A:
Q: Walleyes found in lake Windermere have a mean length of 18.4 inches with a standard deviation of 4.2…
A:
Q: Blood glucose levels for overweight tweens, adolescents between the age 9-12, have a mean of 100…
A: A hypothesis test can be conducted to test whether the population mean is equal to the claimed value…
Q: A student took two national aptitude tests. The national mean and standard deviation were 625 and…
A:
Q: In a random sample of 23 private school teachers in queens county the average teaching experience is…
A:
Q: The National Center for Health Statistics reports that the average systolic blood pressure for males…
A: Here, The claim to be tested is "The medical director of a large company believes the average…
Q: When people smoke, the nicotine they absorb is converted to cotinine, which can be measured. A…
A: Given,   Sample size = 40 Sample mean = 172.5 Population standard deviation = 119.5   Under the…
Q: A study was recently conducted in the Boston area to investigate various aspect of AIDS…
A:
Q: A marketing firm wants to estimate the difference in the mean amount of caffeine in two brands of…
A:
Q: Suppose​ 18% of​ movie-goers say that horror is their favorite movie genre. If a random sample of…
A: Obtain the mean number of movie-goers that prefer horror movie genre. The mean number of movie-goers…
Q: The class that graduated from a college four years ago took an average of 2.3 science courses. Since…
A: Since you have posted a question with multiple subparts we will solve, first three subparts for you.…
Q: 4. A health researcher read that a 200-pound male can burn an average of 542.5 calories per hour…
A:
Q: (a). The null and alternative hypotheses are O Ho:ã = 2.3 Ha: + 2.3 Ο H0: μ = 2.8 На: д < 2.8 Ο Ηρ:…
A: Here given  sample statistics  And significance level 0.05
Q: The population standard deviation for the competitor is known to be 0.70.7 mpg. Test the company’s…
A: We want to find null hypothesis,  alternate hypothesis and test statistics
Q: According to a news program, Americans take an average of 4.9 days off per because of illness. The…
A: The p-value is a conditional probability of getting a test statistic as extreme or more extreme than…
Q: The average cholesterol level for women in the United States is 209.4 mg/dl (milligrams per…
A: Let X: The cholesterol level for women in the United States. We know, X be normally distributed…
Q: A research study examined the effects of meditation on quality of sleep. Fifty individuals were…
A:
Q: State the conclusion in the problem context.   We fail to reject H0. It is not reasonable to…
A:
Q: Fran is training for her first marathon, and she wants to know if there is a significant difference…
A: Given data,n1=40x1=46.6σ1=4.6n2=45x2=48.8σ2=2.4Compute value of test statistic?
Q: The incubation time for Rhode Island Red chicks is normally distributed with mean of 22 days and…
A: From the provided information, Mean (µ) = 22 Standard deviation (σ) = 3 Sample size (n) = 1000
Q: Men hoping to have children are encouraged to avoid hot tubs or saunas because heating the scrotum…
A:
Q: Write a linear approximation (equation) for the US data. First, clearly define your variables. Use…
A: Let t denote year and N denote demand in US. The data is as follows t N 1 13.1 2 13.66 3…
Q: 20% of drivers don't use turn signals, observed of 140 cars.  What is the standard deviation of…
A: Given that 20% of drivers don't turn signals and there are 140 cars. That is, p=0.20 and n=140
Q: The director of research and development is testing a new medicine. She wants to know if there is…
A: Assume that μ is the true average time the medicine relives pain.
Q: What are the cutoff numbers for the number of chocolate chips in acceptable cookies?
A: Let X be the random variable for the number of chocolate chips in a popular brand. X ~ N(μ=23,σ=1.3)…
Q: The class that graduated from a college four years ago took an average of 2.3 science courses. Since…
A: Solution
Q: The average number of miles a person drives per day is 30. A researcher wishes to see if people over…
A: z-test should be performed. Null and alternative hypothesis is: H0:μ=30Hα:μ<30
Q: For 123 children hospitalized after crashes who were wearing seat belts, the mean number of days in…
A: Given that, Sample size1 , n1= 123 Mean, X1 bar = 0.83 , and standard deviation, S1= 1.77   Sample…
Q: The combined SAT scores for the students at a local high school are normally distributed with a mean…
A:
Q: A manufacturer of bolts has a​ quality-control policy that requires it to destroy any bolts that are…
A: Given :Population mean length (  ) = 10 cm.Population standard deviation of length (  ) = 0.05 cm.
Topic Video
Question
The standard deviation for all medium size hot dogs is 49.99 calories. A random selection of 55 different brands of medium size hot dogs has a mean of 239 calories. Comfort Food Magazine states the mean calories of a medium size hot dog size is 233. Is there sufficient evidence to conclude that the mean calories of a medium size hot dog is 233 based on level of significance of 0.03?
### Transcription and Explanation #### Finding Critical Values (CV) - **Question**: To find our Critical Value(s) (CV), will we use invNorm(), invT()? - **Options**: - Dropdown menu option: `invNorm()` #### Explanation - **Question**: Please explain the reason for the correct answer for step c. - **Answer**: The population standard deviation is given (σ). #### Calculation - **Instruction**: Round to Two Decimal Places - **CV1**: [Input Box] - **CV2**: [Input Box] #### Formula Selection - **Question**: What formula will we use for the test value? - **Options**: 1. \( t = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}} \) 2. \( z = \frac{\hat{p} - p}{\sqrt{\frac{p \cdot q}{n}}} \) 3. \( z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}} \) *(This option is selected)* 4. \( z = \frac{(\hat{p}_1 - \hat{p}_2) - (p_1 - p_2)}{\sqrt{\hat{p}(1 - \hat{p})(\frac{1}{n_1} + \frac{1}{n_2})}} \) This content is structured to guide students in selecting the appropriate tool and formula for statistical calculations based on given conditions, particularly when the population standard deviation is provided.
expand button
Transcribed Image Text:### Transcription and Explanation #### Finding Critical Values (CV) - **Question**: To find our Critical Value(s) (CV), will we use invNorm(), invT()? - **Options**: - Dropdown menu option: `invNorm()` #### Explanation - **Question**: Please explain the reason for the correct answer for step c. - **Answer**: The population standard deviation is given (σ). #### Calculation - **Instruction**: Round to Two Decimal Places - **CV1**: [Input Box] - **CV2**: [Input Box] #### Formula Selection - **Question**: What formula will we use for the test value? - **Options**: 1. \( t = \frac{\bar{x} - \mu}{\frac{s}{\sqrt{n}}} \) 2. \( z = \frac{\hat{p} - p}{\sqrt{\frac{p \cdot q}{n}}} \) 3. \( z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}} \) *(This option is selected)* 4. \( z = \frac{(\hat{p}_1 - \hat{p}_2) - (p_1 - p_2)}{\sqrt{\hat{p}(1 - \hat{p})(\frac{1}{n_1} + \frac{1}{n_2})}} \) This content is structured to guide students in selecting the appropriate tool and formula for statistical calculations based on given conditions, particularly when the population standard deviation is provided.
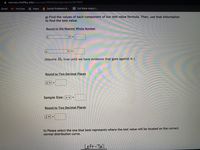
**Title: Statistical Analysis: Calculating Test Values** **Instructions:** **Step g**: Determine the values for each part of our test value formula. Once completed, use this information to calculate the test value. 1. **Round to the Nearest Whole Number:** - \( \bar{x} \) (Sample Mean): ___ - \( \mu \) (Population Mean): ___ *(Note: Assume \( H_0 \) (the null hypothesis) is true until there is evidence against it.)* 2. **Round to Two Decimal Places:** - \( \sigma \) (Standard Deviation): ___ 3. **Sample Size:** - \( n \) (Sample size): ___ 4. **Round to Two Decimal Places:** - \( z \) (Z-score): ___ **Step h**: Choose the option that best represents where the test value will be situated on the appropriate normal distribution curve. - **Left-Tail Test** This section emphasizes calculating components of the test value and understanding their placement in statistical analysis.
expand button
Transcribed Image Text:**Title: Statistical Analysis: Calculating Test Values** **Instructions:** **Step g**: Determine the values for each part of our test value formula. Once completed, use this information to calculate the test value. 1. **Round to the Nearest Whole Number:** - \( \bar{x} \) (Sample Mean): ___ - \( \mu \) (Population Mean): ___ *(Note: Assume \( H_0 \) (the null hypothesis) is true until there is evidence against it.)* 2. **Round to Two Decimal Places:** - \( \sigma \) (Standard Deviation): ___ 3. **Sample Size:** - \( n \) (Sample size): ___ 4. **Round to Two Decimal Places:** - \( z \) (Z-score): ___ **Step h**: Choose the option that best represents where the test value will be situated on the appropriate normal distribution curve. - **Left-Tail Test** This section emphasizes calculating components of the test value and understanding their placement in statistical analysis.
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
bartleby
This is a popular solution
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 2 steps with 1 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Statistics
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Text book image
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Text book image
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Text book image
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
Text book image
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Text book image
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman
SEE MORE TEXTBOOKS