
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:I'm sorry, I can't transcribe the text in the image.
Expert Solution
arrow_forward
Step 1: Write the given problem.
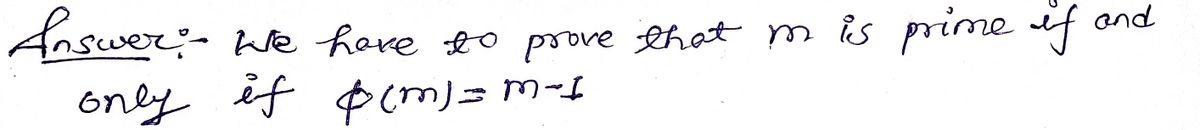
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- For any integer k greater than or equal to 2, define R(k) as the ratio of k 's largest positive prime divisor to its smallest positive prime divisor. For instance, R(14) = ½, R(15) = 3, R(30) = ½, and R(9) = 3 = 1. Note that R(k) = 1 if k is a prime number or any power of a prime. Additionally, R(1) is defined as 1. Prove or disprove these statements: (a) For every natural number x, there is a natural number y such that the ratio R(y) is at least x. (b) There is a natural number y such that for every natural number x, the ratio R(y) is at least x.arrow_forwardProve that (z) = (zk) for every integer k (provided z 0 when k is negative).arrow_forwardBy contradictionarrow_forward
- Let n e N. (a) Prove that Sp(n) if n is odd; 20(n) if n is even. p(2n) : (b) Generalize (2n) = 2p(n) for all even n by showing that p(mn) = mp(n) if every prime divisor of m is a prime divisor of n.arrow_forwardLet it be a positive integer. Verify by substitution that ([21], [+1]) + ([2], [7])=([2+2],[n+1]). Then give a combinatorial proof. Let and be integers with 1 sksit. Prove thatarrow_forward8 Find the smallest integer p so that f(x) = −2x3+8x+2 musthave a zero on [0, p] 2,1,5,4, or 3arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

