(c) Prove that every function f(x) can be written as a sum of an even function and an odd function. For any function f with domain R, define functions E(x) = f(x) + f(-x) and O(x) = f(x)-f(-x), as in parts (a) and (b). Then answers completely.) - E(X) + 10(x) = [(x) + f( [₁0+1 (2x)] )] + 1/[(*)-(-)] ])) + (²x) - ((-x)] O f(x) = (d) Using parts (a), (b), and (c), express the function f(x) = 2*+ (x - 3)2 as a sum of an even function and an odd function. =1/√(2x + x + (x − 3)² + 2x + (x + 3)²) + (2x + (x − 3)² - 2* - (x + 3)²) O Rx) = (2x + (x-3)² - 2x - (x + 3)²) + (2x + (x − 3)² - 2* — (x + 3)²) O f(x) = (2x + (x-3)² + 2* + (x + 3)²) - ¹½ (2* + (x − 3)² – 2x − (x + 3)²) Of(x) = (2x + (x-3)² + 2*+ (x+3)²) - (2x + (x-3)² - 2x - (x + 3)²) O Rx) = (2x + (x-3)² -2°* - (x + 3)²) + ½ (2* + (x − 3)² - 2¯* - (x + 3)²) O f(x) = (2x + (x-3)² + 2¯* + (x + 3)²) + (2* + (x − 3)² - 2-* - (x + 3)²) Eis -Select- 0 is Select, and we show that f(x)=E(x) +10(x). (Simplify your
(c) Prove that every function f(x) can be written as a sum of an even function and an odd function. For any function f with domain R, define functions E(x) = f(x) + f(-x) and O(x) = f(x)-f(-x), as in parts (a) and (b). Then answers completely.) - E(X) + 10(x) = [(x) + f( [₁0+1 (2x)] )] + 1/[(*)-(-)] ])) + (²x) - ((-x)] O f(x) = (d) Using parts (a), (b), and (c), express the function f(x) = 2*+ (x - 3)2 as a sum of an even function and an odd function. =1/√(2x + x + (x − 3)² + 2x + (x + 3)²) + (2x + (x − 3)² - 2* - (x + 3)²) O Rx) = (2x + (x-3)² - 2x - (x + 3)²) + (2x + (x − 3)² - 2* — (x + 3)²) O f(x) = (2x + (x-3)² + 2* + (x + 3)²) - ¹½ (2* + (x − 3)² – 2x − (x + 3)²) Of(x) = (2x + (x-3)² + 2*+ (x+3)²) - (2x + (x-3)² - 2x - (x + 3)²) O Rx) = (2x + (x-3)² -2°* - (x + 3)²) + ½ (2* + (x − 3)² - 2¯* - (x + 3)²) O f(x) = (2x + (x-3)² + 2¯* + (x + 3)²) + (2* + (x − 3)² - 2-* - (x + 3)²) Eis -Select- 0 is Select, and we show that f(x)=E(x) +10(x). (Simplify your
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
100%
![(c) Prove that every function f(x) can be written as a sum of an even function and an odd function.
For any function f with domain R, define functions E(x) = f(x) + f(-x) and O(x) = f(x) = f(-x), as in parts (a) and (b). Then
answers completely.)
1 E(X) + 10(x) = [1(x) + f(
1 [(x) +1
[2x]
[)] + 1/ [~ - - ]
]])) + f(x) = f(-x)}]
(d) Using parts (a), (b), and (c), express the function f(x) = 2*+ (x - 3)2 as a sum of an even function and an odd function.
-²¹ (2x + (x − 3)² + 2²× + (x + 3)²) + ½ (2× + (x − 3)² − 2−× − (x + 3)²)
O f(x) = (2x + (x-3)² - 2x - (x + 3)²) + (2x + (x − 3)² - 2* — (x + 3)²)
O f(x) =
O f(x) = (2x + (x-3)² + 2* + (x + 3)²) - ¹½ (2* + (x − 3)² − 2²* − (x + 3)²)
O f(x) = (2x + (x − 3)² + 2x + (x + 3)²) - (2* + (x − 3)² – 2* − (x + 3)²)
O fx) = (2x + (x-3)² -2¯* - (x + 3)²) + ¹ (2* + (x − 3)² - 27* - (x + 3)²)
O f(x) = (2x + (x-3)² + 2x + (x + 3)²) + (2x + (x − 3)² - 2* - (x + 3)²)
is-Select- ,20 is Select, and we show that f(x)=E(x) +10(x). (Simplify your](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fbe983b18-ee33-44db-82aa-7c6bfcc1e549%2F1f47de0e-7d62-4f23-a5bc-7709e11a6295%2Fmwgy70c_processed.jpeg&w=3840&q=75)
Transcribed Image Text:(c) Prove that every function f(x) can be written as a sum of an even function and an odd function.
For any function f with domain R, define functions E(x) = f(x) + f(-x) and O(x) = f(x) = f(-x), as in parts (a) and (b). Then
answers completely.)
1 E(X) + 10(x) = [1(x) + f(
1 [(x) +1
[2x]
[)] + 1/ [~ - - ]
]])) + f(x) = f(-x)}]
(d) Using parts (a), (b), and (c), express the function f(x) = 2*+ (x - 3)2 as a sum of an even function and an odd function.
-²¹ (2x + (x − 3)² + 2²× + (x + 3)²) + ½ (2× + (x − 3)² − 2−× − (x + 3)²)
O f(x) = (2x + (x-3)² - 2x - (x + 3)²) + (2x + (x − 3)² - 2* — (x + 3)²)
O f(x) =
O f(x) = (2x + (x-3)² + 2* + (x + 3)²) - ¹½ (2* + (x − 3)² − 2²* − (x + 3)²)
O f(x) = (2x + (x − 3)² + 2x + (x + 3)²) - (2* + (x − 3)² – 2* − (x + 3)²)
O fx) = (2x + (x-3)² -2¯* - (x + 3)²) + ¹ (2* + (x − 3)² - 27* - (x + 3)²)
O f(x) = (2x + (x-3)² + 2x + (x + 3)²) + (2x + (x − 3)² - 2* - (x + 3)²)
is-Select- ,20 is Select, and we show that f(x)=E(x) +10(x). (Simplify your
Expert Solution
Step 1
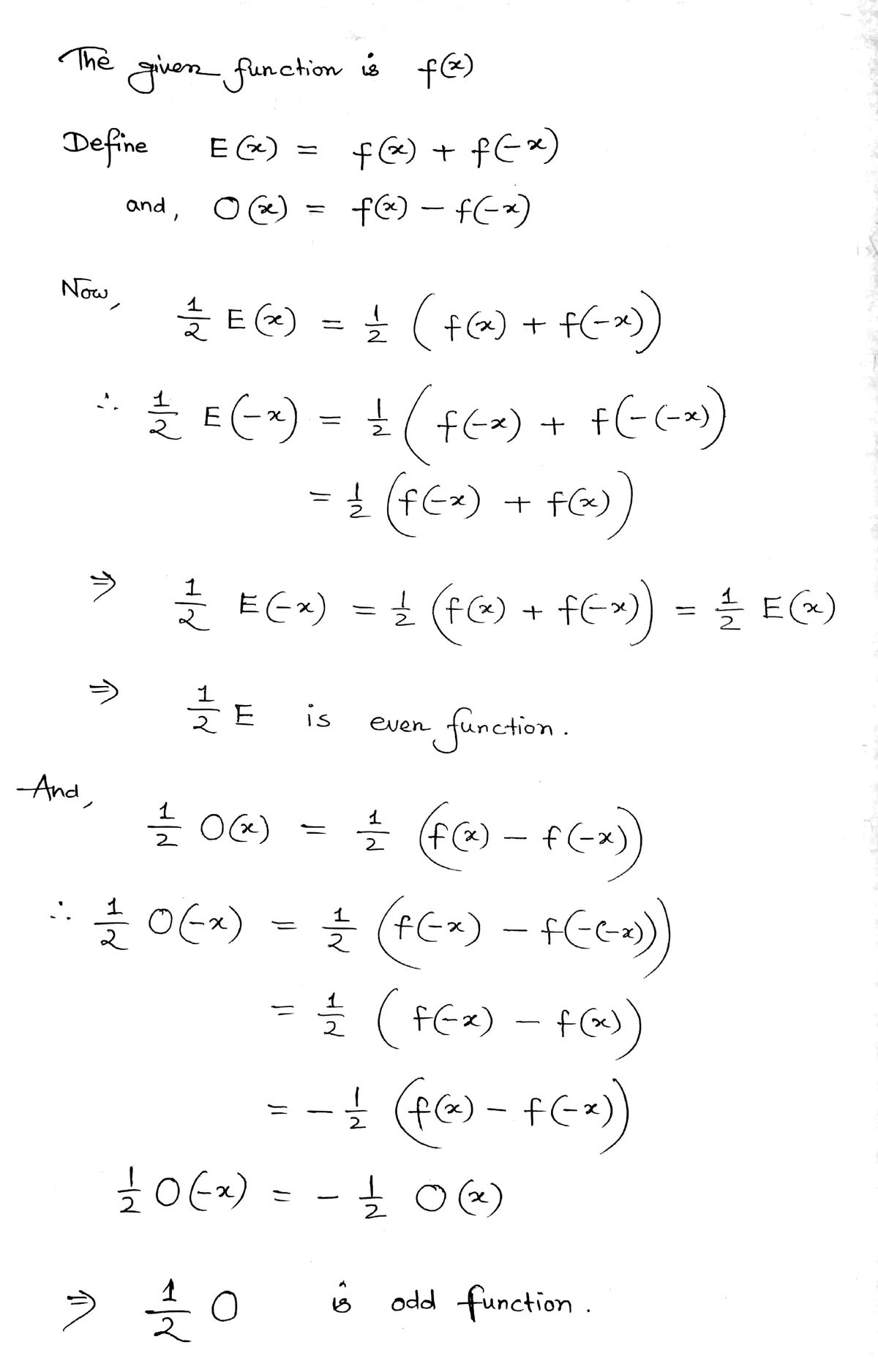
Step by step
Solved in 3 steps with 3 images
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning