
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question
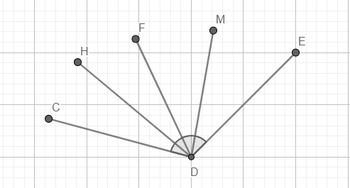
Given: m∠CDE=120∘. DH bisects ∠CDF, DM bisects ∠FDE. Find m∠HDM. Show your work in the space provided below. Explain all steps.
Transcribed Image Text:### Educational Website Content
#### Understanding Angles and Rays
In this lesson, we will explore the concepts of angles and rays through the illustrated diagram.
**Diagram Explanation:**
The provided diagram showcases several rays emanating from a single point, labeled "D." These rays extend outward and are labeled "C," "H," "F," "M," and "E." Each ray represents a line that starts at point D and travels towards the respective points (C, H, F, M, and E).
Here is a detailed breakdown of the diagram:
1. **Point D:**
- This is the central point from which all rays originate.
2. **Rays:**
- **Ray DC:** Extends from point D to point C.
- **Ray DH:** Extends from point D to point H.
- **Ray DF:** Extends from point D to point F.
- **Ray DM:** Extends from point D to point M.
- **Ray DE:** Extends from point D to point E.
3. **Angle Visualization:**
- The diagram also includes an illustration of an angle formed by the rays extending from point D. An arc is drawn between two of the rays (DF and DM) to show the angle at point D.
**Key Concepts:**
- **Rays:** A ray is a part of a line that starts at a particular point and extends infinitely in one direction. In this diagram, all rays start at point D and extend towards their respective points (C, H, F, M, and E).
- **Angles:** An angle is formed by two rays that share a common endpoint. The common endpoint is called the vertex of the angle, and the rays are called the sides of the angle. In this diagram, multiple angles can be formed, such as ∠CDF, ∠FDC, ∠MDF, etc.
- **Measuring Angles:** The size of an angle is measured in degrees (°), and the arc between the rays DF and DM signifies the measured angle at point D.
This diagram is an excellent representation for understanding the basic geometry of rays and angles. It visually illustrates how rays can join at a common point to form angles, which is a foundational concept in geometry.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- You have to slove for x. Please help me and please show your work so I know how to do it.arrow_forwardREVIEW: Find x so that a // b. State the converse used. b (6x - 30)° 96⁰ 北 aarrow_forwardFind the total area of the shaded regions. 25 y=x√ 25-x² 20- N -8 -6 -4 -2 15- 10- LO 5- 15- -10 -15- -20- -25 y 2 4 6 00 ... The total area of the shaded regions is. (Simplify your answer.)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning