
Physics for Scientists and Engineers: Foundations and Connections
1st Edition
ISBN: 9781133939146
Author: Katz, Debora M.
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
Body A in the figure weighs 110 N, and body B weighs 86 N. The coefficients of friction between A and the incline are μs = 0.48 and μk = 0.22. Angle θ is 50°. Let the
positive direction of an x axis be up the incline. What is the acceleration of A if A is initially (a) at rest, (b) moving up the incline, and (c) moving down the incline?
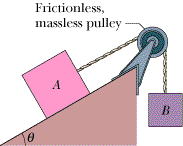
Transcribed Image Text:**Inclined Plane and Pulley System**
**Diagram Explanation for Educational Purposes:**
The diagram illustrates a physics problem involving an inclined plane and a pulley system. Here are the details represented in the diagram:
1. **Objects Involved:**
- **Object A:** This is a block situated on an inclined plane. The block is colored pink.
- **Object B:** This is another block, colored purple, hanging freely in the air.
2. **Inclined Plane:**
- The inclined plane is shown at an angle \( \theta \) to the horizontal ground.
3. **Pulley System:**
- A pulley is depicted at the top right of the inclined plane.
- The pulley is labeled as "Frictionless, massless pulley," indicating that there is no friction in the pulley and it does not contribute any mass to the system.
4. **Connection Between Objects:**
- A rope is shown running over the pulley, connecting Object A and Object B.
- This setup implies that the motion of one object (e.g., moving down the inclined plane) will affect the other's motion (e.g., rising or descending).
**Physics Concepts:**
This system is often used to study concepts such as:
- Newton’s laws of motion.
- Frictionless surfaces (ideal scenarios).
- Tension in the rope.
- Gravitational force components along and perpendicular to the inclined plane.
- Forces and their resultant acceleration on both objects.
This setup can be used to derive equations for the acceleration of the blocks and the tension in the rope considering the angle \( \theta \), masses of blocks A and B, and gravitational constant \( g \).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 7 steps with 7 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A black widow spider hangs motionless from a web that extends vertically from the ceiling above. If the spider has a mass of 1.5 g, what is the tension in the web?arrow_forwardTwo blocks, each of mass m = 3.50 kg, are hung from the ceiling of an elevator as in Figure P4.33. (a) If the elevator moves with an upward acceleration a of magnitude 1.60 m/s2, find the tensions T1 and T2 in the upper and lower strings. (b) If the strings can withstand a maximum tension of 85.0 N, what maximum acceleration can the elevator have before a string breaks? Figure P4.33 Problems 33 and 34.arrow_forwardLet us make the (unrealistic) assumption that a boat of mass m gliding with initial velocity v0 in water is slowed by a viscous retarding force of magnitude bv2, where b is a constant, (a) Find and sketch v(t). How long does it take the boat to reach a speed of v0/l000? (b) Find x(t). How far does the boat travel in this time? Let m = 200 kg, v0 = 2 m/s, and b = 0.2 Nm-2s2.arrow_forward
- If a single constant force acts on an object that moves on a straight line, the objects velocity is a linear function of time. The equation v = vi + at gives its velocity v as a function of time, where a is its constant acceleration. What if velocity is instead a linear function of position? Assume that as a particular object moves through a resistive medium, its speed decreases as described by the equation v = vi kx, where k is a constant coefficient and x is the position of the object. Find the law describing the total force acting on this object.arrow_forwardIf the vector components of the position of a particle moving in the xy plane as a function of time are x(t)=(2.5ms2)t2i and y(t)=(5.0ms3)t3j, when is the angle between the net force on the particle and the x axis equal to 45?arrow_forwardA force F applied to an object of mass m1 produces an acceleration of 3.00 m/s2. The same force applied to a second object of mass m2 produces an acceleration of 1.00 m/s2. (a) What is the value of the ratio m1/m2? (b) If m1 and m2 are combined into one object, find its acceleration under the action of the force F.arrow_forward
- A 3.00-kg block starts from rest at the top of a 30.0 incline and slides a distance of 2.00 m down the incline in 1.50 s. Find (a) the magnitude of the acceleration of the block, (b) the coefficient of kinetic friction between block and plane, (c) the friction force acting on the block, and (d) the speed of the block after it has slid 2.00 m.arrow_forwardA bag of cement weighing 325 N hangs in equilibrium from three wires as suggested in Figure P4.23. Two of the wires make angles 1 = 60.0 and 2 = 40.0 with the horizontal. Assuming the system is in equilibrium, find the tensions T1, T2, and T3 in the wires. Figure P4.23 Problems 23 and 24.arrow_forwardA sleigh is being pulled horizontally by a train of horses at a constant speed of 8.05 m/s. The magnitude of the normal force exerted by the snow-covered ground on the sleigh is 6.37 103 N. a. If the coefficient of kinetic friction between the sleigh and the ground is 0.23, what is the magnitude of the kinetic friction force experienced by the sleigh? b. If the only other horizontal force exerted on the sleigh is due to the horses pulling the sleigh, what must be the magnitude of this force?arrow_forward
- Figure P4.26 shows loads hanging from the ceiling of an elevator that is moving at constant velocity. Find the tension in each of the three strands of cord supporting each load. Figure P4.26arrow_forwardTwo blocks, each of mass m, are hung from the ceiling of an elevator as in Figure P4.33. The elevator has an upward acceleration a. The strings have negligible mass. (a) Find the tensions T1 and T2 in the upper and lower strings in terms of m, a, and g. (b) Compare the two tensions and determine which string would break first if a is made sufficiently large. (c) What are the tensions if the cable supporting the elevator breaks? Figure P4.33 Problems 33 and 34.arrow_forwardTwo forces F1=(62.98i15.80j) N and F2=(23.66i78.05j) are exerted on a particle. The particles mass is 14.23 kg. a. Find the particles acceleration in component form. b. What are the magnitude and direction of the acceleration?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning

Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning

Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning

Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Glencoe Physics: Principles and Problems, Student...
Physics
ISBN:9780078807213
Author:Paul W. Zitzewitz
Publisher:Glencoe/McGraw-Hill

College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning