
A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question

Transcribed Image Text:Big houses: The U.S. Census Bureau reported that the mean area of U.S. homes built in 2018 was 2559 square feet. Assume that a
simple random sample of 17 homes built in 2020 had a mean area of 2592 square feet, with a standard deviation of 179 square feet.
Assume the population of areas is normally distributed. Can you conclude that the mean area of homes built in 2020 is not equal to that
of homes built in 2018 ? Use the a=0.01 level of significance.
H: µ=2559
H: u#2559
Part 1 of 3
(a) Find the P-value. Use the TI-84 calculator and round your answer to at least four decimal places.
The P-value is
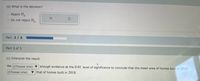
Transcribed Image Text:(b) What is the decision?
O Reject Ho
Do not reject H,
Part: 2/ 3
Part 3 of 3
(c) Interpret the result.
We (Choose one) ▼ enough evidence at the 0.01 level of significance to conclude that the mean area of homes built in 2020
(Choose one)
▼ that of homes built in 2018.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- Most medical schools require applicants for admission to take the Medical College Admissions Test (MCAT) examination. Scores on the MCAT are roughly normally distributed with a mean of 500 and a standard deviation of 10.6. What percentage of students score above 518 points? ( write as a decimal and round to the nearest hundredth)arrow_forwardThe income of trainess at a local mill are normally distributed with a mean of $1100 and a standard deviation of $150. What percentage of trainees earn less than $900 a month?arrow_forwardAn analyst found that the average amount of money in bank accounts at his/her bank is $2,000 with a standard deviation of $150. What would be the variance?arrow_forward
- A company wants to assess the average time it takes for customers to complete a particular task on their website. They collect the following data from a sample of 10 customers: 5, 6, 7, 8, 9, 10, 10, 11, 12, 13 minutes. Calculate the sample mean and standard deviation for this data.arrow_forwardA person in the U.S. eats about 25 pounds of M&M's per year with a standard deviation of 3 pounds. How many M&M's would I have to eat to be in the 3rd quartile?arrow_forwardUse the Empirical Rule. The mean speed of a sample of vehicles along a stretch of highway is 68 miles per hour, with a standard deviation of 3 miles per hour. Estimate the percent of vehicles whose speeds are between 65 miles per hour and 71 miles per hour. (Assume the data set has a bell-shaped distribution.) Approximately nothing% of vehicles travel between 65 miles per hour and 71 miles per hour.arrow_forward
- A sociologist found that in a sample of 45 retired men, the average number of jobs they had during theirlifetimes was 7.2. The population standard deviation is 2.3(a) Find the best point estimate of the mean.The best point estimate of the mean isarrow_forwardFor a random sample of 10 men, the mean head circumferences are x-bar = 57.3 cm, and the sample standard deviation is s = 2cm. what is the standard error of the mean?arrow_forwardThe average McDonald's restaurant generates $2.6 million in sales each year with a standard deviation of 1. Tatiana wants to know if the average sales generated by McDonald's restaurants in Alaska is different than the worldwide average. She surveys 25 restaurants in Alaska and finds the following data (in millions of dollars):3.2, 1.8, 0.9, 3.2, 3.6, 1.7, 4.2, 2, 3.1, 3.9, 3, 2.9, 2.5, 3.5, 3, 3, 2.4, 5, 3.8, 0.9, 2.2, 2.4, 2.6, 2.8, 3.3Perform a hypothesis test using a 10% level of significance. Find the pp-value of the point estimate. P(p( <or > )= P(z<)=P( ? )=)=? p value =?pp-value==arrow_forward
- The ages of the employees at Solar Systems, Inc. is normally distributed with a mean of 32.7 years and a standard deviation of 1.8 years. What percentage of employees at Solar Systems, Inc. are younger than 30 years old? Round your answer to the nearest tenth of a percent.arrow_forwardjoans finishing time for the bolder boulder 10k race was 1.77 standard deviations faster than the womens average for her age group. there were 415 women in her group. assuming a normal distribution, how many women ran faster than joan? rounded down to the nearest whole numberarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON

A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON
