An Introduction to Physical Science
An Introduction to Physical Science
14th Edition
ISBN: 9781305079137
Author: James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar Torres
Publisher: Cengage Learning
Bartleby Related Questions Icon

Related questions

Q: A bead of mass m slides without friction along a curved wire with shape z = f(r) x² + y?, i.e. the…
A: The force perpendicular to plane of wire is obtained by imposing the constraint condition ϕ=ωt using…
Q: A variation of the amusement park ride discussed in Problem 11 is the Gravitron, which consists of a…
A:
Q: A satellite is placed in a geosynchronous orbit. In this equatorial orbit with a period of 24 hours,…
A: Given that a satellite is placed in a geosynchronous orbit. In this equatorial orbit with a period…
Q: A ball of mass m is swung in a vertical circle on a string of length L in the clockwise direction,…
A:
Q: Review | Constants a mass moving in a circle of radius R with angular velocity w. =R cos(ust)i +…
A: Given: r(t)=Rcosωt i^ +Rsinωt j^
Q: out the z-axis for ant 5.
A: Given: The value of z is 2 and the constant value is 5.
Q: Determine the moment produced by force FB about point O. Express the result as a Cartesian vector.…
A: The position vector rOA and force vector FB is given as,
Q: If we model a blade as a point mass at the midpoint of the blade, what is the inward force necessary…
A:
Q: A basketball, which can be modelled as a hollow sphere (Icm = (2/3)MR2 ) of mass M and radius R,…
A: Let the mass = M Let the radius = R vo = 4.01 m/s
Q: Calculate the magnitude of the angular momentum, in kg.m.s-2,for a particle with a position vector…
A:
Q: What is the torque on the shell, about the origin, as a function of time! What is the angular…
A:
Q: A solid sphere of radius R is placed at a height of 35 cm on a 15° slope. It is released and rolls,…
A:
Q: Two ladybugs are riding on a turntable as it rotates at 15 rpm as shown in (Figure 1). Figure 10 cm…
A:
Q: one end of a cord is fixed and a small 0.5 kg object is attached to the other end , where it swings…
A: Solution:   Given Values,   Mass (m)=0.5 Kg Radius (r)=2 m  Speed (v)=8 m/sAngle (θ)=200
Q: Describe the radial acceleration, tangential acceleration, and total acceleration vectors for a…
A: Let the radius of the point from the centre of the disk is r. The angular velocity is denoted by ω.…
Q: h R You are building a display for a children's science museum in which a uniform, solid sphere of…
A:
Q: The smooth circular bar rotates with constant angular velocity wo about the vertical axis AB. The…
A: Given Data: The radius of the circular bar is R=0.5m.The angular position where the mass is…
Q: Draw separate free-body diagrams of the forces on the stopper and the forces on the hanging…
A: (3) Introduction: A free-body diagram is a graphical illustration used to visualize the applied…
Q: A 3.80 kg rock has a horizontal velocity of magnitude 12.0 m/s when it is at point P in the figure…
A:
Q: A small block on a frictionless horizontal surface has a mass of 0.0200 kg. It is attached to a…
A:
Q: I Review | Constants A flywheel with a radius of 0.230 m starts from rest and accelerates with a…
A: The given data are listed below with appropriate variables. Here, r denotes the radius, ωi denotes…
Q: A particle of mass 1.50 kg is moving with velocity v = (7.6î + 6.0ĵ) m/s. Part A Find the angular…
A:
Q: Determine the angular velocity, WAB, of link AB and the velocity, vB, of collar B for the instant…
A: Explanation Given below:
Q: rotating from rest with a constant angular acceleration. It takes 2.5 seconds to complete ten…
A:
Q: Consider an annular disk rolling down an inclined plane. The annular disk has mass 154 [g], inner…
A: Given: mass of annular disk, m = 154g inner radius, r= 8 cm outer radius, R=12 cm angle, θ = 44.60…
Q: consider the figure above. consider the small block (M). et say that this inverted cone is rotating…
A:
Q: A car initially traveling eastward turns north by traveling in a circular path at uniform speed as…
A:
Q: In the space below, make a sketch of angular displacement, , as a function of time as you slowly and…
A: Angular displacement of a body is the revolution  made through a point around a center or the line…
bartleby

Concept explainers

Rigid Body
A rigid body is an object which does not change its shape or undergo any significant deformation due to an external force or movement. Mathematically speaking, the distance between any two points inside the body doesn't change in any situation.
Rigid Body Dynamics
Rigid bodies are defined as inelastic shapes with negligible deformation, giving them an unchanging center of mass. It is also generally assumed that the mass of a rigid body is uniformly distributed. This property of rigid bodies comes in handy when we …
Question

Below is a sketch of the toy on a rotor ride at the moment after the floor drops. The rotor has a radius of R and the toy has mass m. Assume the angular velocity is constant, and the toy is not slipping downward.

write Newton’s Second Law for the x and y directions.

Use algebra and your equations above to predict the minimum angular velocity ωmin​ necessary to keep the toy “stuck” to the side of the rotation tube. Express your answer in terms of g, μs, R. (nonumbers yet). Show all of your work and your final result below.

R Toy
expand button
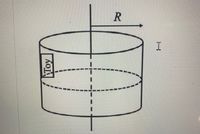
Transcribed Image Text:R Toy
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
bartleby
This is a popular solution
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 2 steps with 1 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Physics
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
An Introduction to Physical Science
Physics
ISBN:9781305079137
Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar Torres
Publisher:Cengage Learning
Text book image
College Physics
Physics
ISBN:9781938168000
Author:Paul Peter Urone, Roger Hinrichs
Publisher:OpenStax College
Text book image
Glencoe Physics: Principles and Problems, Student...
Physics
ISBN:9780078807213
Author:Paul W. Zitzewitz
Publisher:Glencoe/McGraw-Hill
Text book image
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Text book image
Inquiry into Physics
Physics
ISBN:9781337515863
Author:Ostdiek
Publisher:Cengage
Text book image
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
SEE MORE TEXTBOOKS