Below are the average heights for American boys in 1990. Age (years) Height (cm) birth 50.8 2 83.8 3 91.4 5 106.6 119.3 10 137.1 14 157.5 O Part (a) O Part (b) O Part (c) O Part (d) Calculate the least squares line. Put the equation in the form of: ŷ = a + bx. (Round your answers to three decimal places.) ý = O Part (e) Find the correlation coefficient r. (Round your answer to four decimal places.) r= Is it significant? Yes O No O Part (f) Find the estimated average height for a one-year-old. (Use your equation from part (d). Round your answer to one decimal place.) cm Find the estimated average height for a eleven-year-old. (Use your equation from part (d). Round your answer to two decimal places.) cm O Part (g) Does it appear that a line is the best way to fit the data? Why or why not? O A line does appear to be the best way to fit the data because the data points follow a positive linear trend. O A line is not the best way to fit the data because it does not touch all the data points. O A line is the best way to fit the data because there is only one correct line that will fit a data set. O A line is the best way to fit the data because the slope of the line is positive and the linear correlation is positive.
Below are the average heights for American boys in 1990. Age (years) Height (cm) birth 50.8 2 83.8 3 91.4 5 106.6 119.3 10 137.1 14 157.5 O Part (a) O Part (b) O Part (c) O Part (d) Calculate the least squares line. Put the equation in the form of: ŷ = a + bx. (Round your answers to three decimal places.) ý = O Part (e) Find the correlation coefficient r. (Round your answer to four decimal places.) r= Is it significant? Yes O No O Part (f) Find the estimated average height for a one-year-old. (Use your equation from part (d). Round your answer to one decimal place.) cm Find the estimated average height for a eleven-year-old. (Use your equation from part (d). Round your answer to two decimal places.) cm O Part (g) Does it appear that a line is the best way to fit the data? Why or why not? O A line does appear to be the best way to fit the data because the data points follow a positive linear trend. O A line is not the best way to fit the data because it does not touch all the data points. O A line is the best way to fit the data because there is only one correct line that will fit a data set. O A line is the best way to fit the data because the slope of the line is positive and the linear correlation is positive.
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
Please label each part
SUBPART
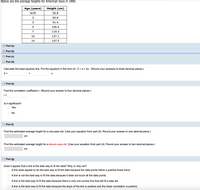
Transcribed Image Text:Below are the average heights for American boys in 1990.
Age (years)
Height (cm)
birth
50.8
2
83.8
3
91.4
5
106.6
7
119.3
10
137.1
14
157.5
+ Part (a)
+ Part (b)
+ Part (c)
Part (d)
Calculate the least squares line. Put the equation in the form of: ý = a + bx. (Round your answers to three decimal places.)
%3D
Part (e)
Find the correlation coefficient r. (Round your answer to four decimal places.)
r =
Is it significant?
Yes
No
O Part (f)
Find the estimated average height for a one-year-old. (Use your equation from part (d). Round your answer to one decimal place.)
cm
Find the estimated average height for a eleven-year-old. (Use your equation from part (d). Round your answer to two decimal places.)
cm
O Part (g)
Does it appear that a line is the best way to fit the data? Why or why not?
A line does appear to be the best way to fit the data because the data points follow a positive linear trend.
A line is not the best way to fit the data because it does not touch all the data points.
A line is the best way to fit the data because there is only one correct line that will fit a data set.
A line is the best way to fit the data because the slope of the line is positive and the linear correlation is positive.
O O O O
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 1 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Recommended textbooks for you
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON
The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman