Question
I got the first two parts correct but the last I am struggling with my strategy so far is using the intensity=watts/area formula with 8.680e+09 V/m as the intensity of the wattage I found previously and the area I am using the diameter form of the circle equation. then I used algebra to solve. The issue I believe is that 8.680e+09 V/m is not in the right units but am not sure where to progress from there.
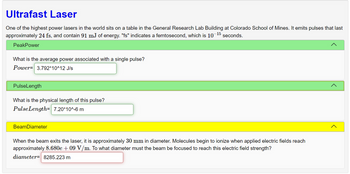
Transcribed Image Text:**Ultrafast Laser**
One of the highest power lasers in the world is located at the General Research Lab Building at Colorado School of Mines. It emits pulses lasting approximately 24 femtoseconds (fs) and containing 91 millijoules (mJ) of energy. Here, "fs" denotes a femtosecond, which is \(10^{-15}\) seconds.
---
**Peak Power**
- **Question:** What is the average power associated with a single pulse?
- **Answer:** \( \text{Power} = 3.792 \times 10^{12} \, \text{J/s} \)
---
**Pulse Length**
- **Question:** What is the physical length of this pulse?
- **Answer:** \( \text{PulseLength} = 7.20 \times 10^{-6} \, \text{m} \)
---
**Beam Diameter**
When the beam exits the laser, it has a diameter of approximately 30 mm. Molecules start to ionize when applied electric fields reach approximately \( 8.680 \times 10^9 \, \text{V/m} \). The beam must be focused to a diameter of 8285.223 m to reach this electric field strength.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps

Knowledge Booster
Similar questions
- The question is whether these relationships are linear or non-linear, can you please inform me on how I'd be able to tell?arrow_forward8.36 grams of a mystery substance of food with a molar mass of 149.36 g/mol is burned in a bomb calorimeter. The water in the bomb calorimeter absorbs 105,961 Joules from the burning of the substance. Calculate the heat of combustion of the mystery substance in kJ/mol. (Please input your answer as a negative number.) (DO NOT PUT UNITS IN YOUR ANSWER.) Assume that all of the heat lost by the substance is transferred to the water and no heat is lost to the surroundings.arrow_forwardUsing your values for 7, calculate the average period Ibar (I) and its standard error. How does the error on the average period /bar (T) compares to the errors on the periods, I? What can you do to reduce the uncertainty on /bar (T)? What can you do to reduce the uncertainty on 7 ? Peried Trial T AT 4 141 $ 10.69 +α-0.5 2 10.60 + or -0.5 2 10.40 +α-0.5 10.43 +α-0.5 S 10.37 + or -0.5 Using your values for T, calculate the average period 7 and its standard error How does the error on the garage period compares to the errors on the periods, 7? What can you do to reduce the uncertainty on 7? What can you do to reduce the uncertainty on T7arrow_forward
- When coverting metric measures I am having a hard time understanding the coversion concept?arrow_forwardPlease help me with these problems. We are using algebra based physics, not calc basedarrow_forwardA marathon runner completes a 42.188-km course in 2 h, 35 min, and 39 s. There is an uncertainty of 28 m in the distance traveled and an uncertainty of 1 s in the elapsed time. (Give all answers to the appropriate number of significant figures. Note that uncertainties should be reported to one significant figure and percent uncertainties should be reported to two significant figures.) (a) Calculate the percent uncertainty in the distance. _________% (b) Calculate the percent uncertainty in the elapsed time. __________%arrow_forward
- Plz only solve part d and h... plz solve it correctlyarrow_forwardA hot tub with a surface area of 28 ft2 is filled with water to a depth of 29 in . Hint: volume is calculated as area × height (A × h). A) What is the volume of water in the tub, in liters? Express your answer to two significant figures and include the appropriate units. B) How many kilojoules are needed to heat the water from 59∘F to 103 ∘F? Express your answer to two significant figures and include the appropriate units. C) If the hot-tub heater provides 5900 kJ/min, how long, in hours, will it take to heat the water in the hot tub from 59∘F to 103∘F? Express your answer to two significant figures and include the appropriate units.arrow_forwardThe temperature at a point (x, y) is T(x, y), measured in degrees Celsius. A bug crawis so that its position after t seconds is given by where x and y are measured in centimeters. The temperature function satisfles T3, 6) 2 and T(3, 6) -7. How fast is the temperature rising on the bug's path after 2 seconds? (Round your answer to two decimal places.) C/s Need Help? Read Watch Master tarrow_forward
arrow_back_ios
arrow_forward_ios