
Elements Of Electromagnetics
7th Edition
ISBN: 9780190698614
Author: Sadiku, Matthew N. O.
Publisher: Oxford University Press
expand_more
expand_more
format_list_bulleted
Question
Considering the results in Table 1, and the documentation in the image too, please calculate the dynamic viscosity for the fluids listed in Table 3.
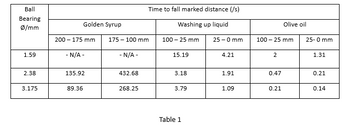
Transcribed Image Text:Ball
Bearing
Ø/mm
1.59
2.38
3.175
Golden Syrup
200- 175 mm
- N/A -
135.92
89.36
175-100 mm
- N/A -
432.68
Time to fall marked distance (/s)
Washing up liquid
268.25
100- 25 mm
15.19
3.18
3.79
Table 1
25-0 mm
4.21
1.91
1.09
100 - 25 mm
2
0.47
Olive oil
0.21
25-0 mm
1.31
0.21
0.14

Transcribed Image Text:Exercise B - Measurement of Viscosity
Objective
To determine the viscosity of various liquids at atmosphere pressure and temperature.
Background theory
Viscosity is a measure of a fluid's resistance to flow. It describes the internal friction of a moving
fluid or can be described as the friction that a fluid will exert on an external object as travels in
that fluid medium. The theory behind this experiment is as follows:
From the Figure 2; when the ball is moving with a uniform velocity u, then forces acting on the
sphere are:
a. the gravitational force on the ball mg.
b. the buoyant force or upthrust FB
c. the viscous force resisting motion Fy
Since the velocity of fall is uniform, then algebraic sum of these forces must be zero.
mg - FB-Fv=0
The gravitational force on the ball can be calculated as:
4
mg = Ps9 3
where
Ps= density of ball,
r = radius of sphere.
The buoyant force can be calculated as:
4
FB = P193
P193
πr.²
πr²
where
P1 = density of liquid.
Fv=6yX₂
The viscous force from Stokes Law can be calculated as:
Where
μ = coefficient of viscosity,
u = mean velocity of ball.
4
μ =
-
Ps9²₁².
Results
4πr³g
3x6πμru
u=
==
쓰
V =
Calculate the velocity of the ball passing through the marked distances (between 100 to 25 and
25 to 0) using Equation 4 and find the average.
Distance through which ball falls
Time
4
Liquid
Water
πρ3 – 6πμru = 0
Calculate the average Dynamic viscosity for three different diameter balls passing through each
liquid.
Complete Table 3 for Dynamic Viscosity.
Calculate Kinematic Viscosity by considering density of the liquids found in the first experiment
A (Table 2) using the following equation:
(Ps - P₁) = ²/r² g (Ps-P₁)
u
Barometric pressure 774.0635 mm Hg.
Temperature 16°C.
Specific gravity of steel: 7.8
Olive oil
washing up liquid
Golden Syrup
Equation 3
Table 3. Results for Dynamic and Kinematic Viscosity
Dynamic Viscosity, μ (kg/ms)
Using equation 3
Equation 4
Equation 5
Kinematic Viscosity, v (m²/s)
Using equation 5
SAVE
AI-Generated Solution
info
AI-generated content may present inaccurate or offensive content that does not represent bartleby’s views.
Unlock instant AI solutions
Tap the button
to generate a solution
to generate a solution
Click the button to generate
a solution
a solution
Knowledge Booster
Similar questions
- 2.27 Fluids of viscosities µ1 = 0.1 N s/m2 and 42 = 0.15 N s/m2 are contained between two plates (each plate is 1 m? in area). The thicknesses are h1 = 0.5 mm and h2 = 0.3 mm, respectively. And the upper plate moves at a velocity of 1.5 m/s. Determine the force required to move the upper plate and the fluid velocity at the interface between the two fluids. F, V h2 H2 h1 P2.27 Hint: Both Velocity and Shear stress are continuous at the fluid-fluid interface.arrow_forwardIn a rotary viscometer the radii of the cylinders are respectively 50 mm and 50.5 mm, and the outer cylinder is rotated steadily at 30 rad s. For a certain liquid the torque is 0.45 N-m when the depth of the liquid is 50 mm and the torque is 0.81 N-m when the depth is 100 mm. Estimate the dynamic viscosity of the liquid.arrow_forwardFor the conic body shown in Figure (3) which rotating with constant angular velocity of 12 rad/s, find the torque, which effected by viscosity of the oil that surrounding the conic body if the cone has radius of 4 in, height of 10 in and oil viscosity is 3.125x10" lb.s/in'. Derive all the required equations? 0.01-in film Figure (3) 0.01 inarrow_forward
- List the various types of fluid. Define kinematic viscosity and compressibility. Note the expression of capillary fall as well.arrow_forwardFind the dynamic and kinematic viscosities of kerosene, SAE 10W-30 motor oil, and water at a temperature of 38°C (100°F). show solution.arrow_forwardQuestion 1: Define and state the viscosity equation for a Coutte flow. Question 2: Develop and algebraic equation for viscosity of a liquid as a function of temperature. Calculate the kinematic viscosity of water at T = 303 K. Question 3: If a liquid water at 300C is flowing in a pipe and the pressure drops to the vapor pressure, what happens in the water and why, explain?arrow_forward
- Solve it correctly please.arrow_forwardSolve with explanationarrow_forwardA shaft of diameter 0.35 m rotates at 200 r.p.m. inside a sleeve 100 mm long. The dynamic viscosity of lubricating oil in the 2 mm gap between sleeve and shaft is 8 poises. Calculate the power lost in the bearing.arrow_forward
- Solve fastarrow_forwardProblem 2 The apparatus sketched in the figure below serves as a viscometer i.e. it can be used to measure the viscosity of a liquid. In the drawing, D is a large reservoir containing a viscous liquid A and E is a cylindrical tube of radius R, open at both ends, surrounding and coaxial with B, which is a cylindrical "bob" of radius êR that is dragged up through the fluid by a frictionless pulley system (C) utilizing a weight W. Determine a design equation that relates the viscosity of the liquid to the geometry of the system and the weight W. Hint: you can assume that the length of the cylindrical tube is sufficiently long for the flow to reach steady state. W E D Barrow_forward2.4-2. Shear Stress and Shear Rate in Fluids. Using Fig. 2.4-1, the lower plate is being pulled at a relative velocity of 0.40 m/s greater than the top plate. The fluid used is water at 24°C. a. How far apart should the two plates be placed so that the shear stress t is 0.30 N/m^2? Also, calculate the shear rate. b. If oil with a viscosity of 2.0 x 10^-2 Pa•s is used instead at the same plate spacing and velocity as in part (a), what is the shear stress and the shear rate?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY

Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education

Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning

Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY