
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
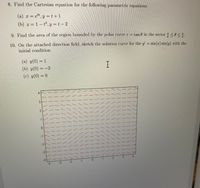
Transcribed Image Text:**Exercises for Chapter Review**
8. **Find the Cartesian equation for the following parametric equations:**
(a) \( x = e^{2t}, \, y = t + 1 \)
(b) \( x = 1 - t^2, \, y = t - 2 \)
9. **Find the area of the region bounded by the polar curve** \( r = \tan \theta \) **in the sector** \( \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3} \).
10. **On the attached direction field, sketch the solution curve for the** \( y' = \sin(x) \sin(y) \) **with the initial condition:**
(a) \( y(0) = 1 \)
(b) \( y(0) = -2 \)
(c) \( y(0) = 0 \)
**Direction Field Diagram Explanation:**
The diagram displays a direction field, which consists of small arrows or line segments indicating the slope of the solution curves at various points in the coordinate plane. The grid spans from \(-3\) to \(4\) on both the x and y axes. The red arrows suggest the behavior of solutions to the differential equation \( y' = \sin(x) \sin(y) \) at given points, showing how the slope varies across different regions of the plane.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- You are watching your friend ride a Ferris wheel whose radius is 40 feet and center at (0,43). When you start watching your friend at t=0, they are at the highest point of the Ferris wheel. You notice the wheel is spinning clockwise at a rate of 120 seconds per revolution. Create a parametric equation that represents your friend's position at t seconds. DO NOT USE A CALCUATOR.arrow_forwardUse t = 4x + 1 to write the parametric equations that can represent y = 12x + 5. %| )x =;y = 31 – 2 x = 4t – 1; y = 481 + 7 ) x = y = 3t + 2 ) x =; y = 3t + 2 4arrow_forwardFind the parametric equation of the line segment from A(1,2,3) to B(5.0, 1), where for t = 0 you are at point A and for t= 1 at point B..arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning